Реферат: Микроволновый фон космоса как суммарное излучение всех звезд

получаем

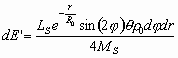. (10)

Световой поток от всего слоя будет равен интегралу:

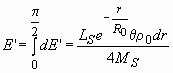. (11)

Суммарный же световой поток от всех звёзд полусферы получится путём интегрирования (11) по расстоянию от нуля до бесконечности:

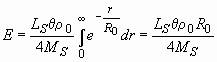. (12)

Поскольку существует связь между интегральной излучательной способностью материального тела и его температурой в соответствии с формулой

, (13)

где — постоянная Стефана-Больцмана, то температура суммарного излучения всех звёзд Вселенной будет определяться выражением

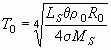. (14)

Известно, что масса средней звезды равна примерно 0,4 массы Солнца. Тогда, если в формулу (14) подставить значения этой массы кг и соответствующую ей светимость звезды Вт, , а также Вт.м-2.К-4 и значение кг/м3 (т. е. ), то для температура равновесного излучения всех звёзд будет равна К, что согласуется с реальными измерениями этой величины ( К).

2. Спектр суммарного излучения звёзд

Как известно, спектр наблюдаемого микроволнового фонового излучения соответствует спектру излучения абсолютно чёрного тела. Распределение же энергии в спектре излучения абсолютно чёрного тела в зависимости от частоты и температуры тела описывается формулой Планка

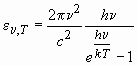, (15)

где: — постоянная Планка; — постоянная Больцмана.

Существует несколько способов вывода формулы (15), но в настоящее время практически общепринят способ, в основе которого лежит распределение Гиббса. Согласно данному распределению, в состоянии теплового равновесия вероятность обнаружить любое состояние частиц макроскопического тела определяется только их полной энергией. Вероятность обнаружить состояние частиц с полной энергией из интервала () равна

. (16)

Если из (1) мы рассмотрим функцию

, (17)

то обнаружим полную аналогию исходных позиций при выводе формулы распределения энергии в спектре излучения абсолютно чёрного тела и формулы спектральной плотности суммарной энергии излучения всех тел Вселенной.

Поскольку каждая звезда имеет свой спектр электромагнитного излучения, подчиняющийся формуле (15), то для облегчения рассуждений можно усреднить (унифицировать) все звёзды. С другой стороны, чем дальше находится сферически-симметричный слой пространства Вселенной с вкрапленными в него звёздами, тем больше его спектр сдвинут в длинноволновую сторону в соответствии с законом (1). Поэтому конечный результат будет представлять собой интеграл

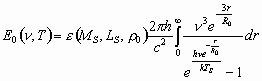, (18)

где — функция, зависящая от массы и светимости средней звезды, а также от средней плотности Вселенной; — температура этой осреднённой звезды.

Для численного исследования поведения интеграла (18) удобнее воспользоваться системой координат, в которой все его постоянные параметры равны 1, т. е. представить интеграл в виде

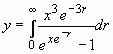. (19)

Рис. 2. Спектр суммарного излучения звёзд (в условных единицах)

Численные исследования показали, что распределение (19) носит характер спектральной плотности излучения абсолютно чёрного тела (рис. 2). Более того, оно точно (в пределах точности численного интегрирования) аппроксимируется функцией

, (20)

которая в соответствующей системе координат тождественна закону Планка (15).