Реферат: Модель рассеяния электромагнитной волны параллелепипедом из диэлектрика с потерями
![]() , (5)
, (5)
причем считаем, что каждая электромагнитная волна при | y | £b удовлетворяет следующим соотношениям:
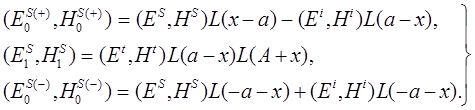 (6)
(6)
Здесь: L(x) - ступенчатая функция:
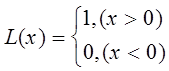 (7)
(7)
Смысл индексов, которыми снабжены каждая из электромагнитных волн, как видно из формул (6), определяющих эти электромагнитные волны, заключается в следующем. Нижний индекс «0»соответствует тому, что поле удовлетворяет волновому уравнению в вакууме, а индекс «1» - тому, что поле удовлетворяет волновому уравнению в среде с потерями. Другими словами, эти индексы соответствуют значениям индекса j =0, 1 в уравнениях (3). Кроме того, верхний значок (+) указывает на то, что данное поле имеет смысл только при x >a , а значок (-) - на то, что рассматриваемое поле имеет смысл только при x <-a . В силу этих определений делаются особенно ясными аналитические свойства Фурье-компонент каждой электромагнитной волны и становится возможным выполнение исследования, основанного на теоретико-функциональных рассуждениях.
Найдем теперь Фурье-компоненты рассеянной волны. Прежде всего посредством перехода к прямому преобразованию Фурье в волновом уравнении (3) при | y | ³b можно получить следующее уравнение:
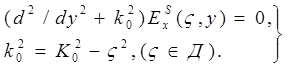 (8)
(8)
Решение этого уравнения, удовлетворяющее граничным условиям (В1), (В2), может быть записано следующими образом:
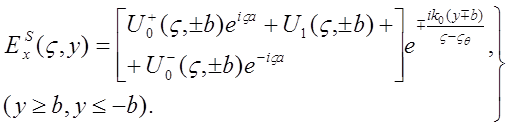 (9)
(9)
Считаем здесь, что ветвление ![]() выбирается условием
выбирается условием ![]() . Кроме того, неизвестные функции представляют собой, как показывают приводимые ниже формулы, Фурье-компоненты рассеянной волны при | y | = b . Наконец, точка
. Кроме того, неизвестные функции представляют собой, как показывают приводимые ниже формулы, Фурье-компоненты рассеянной волны при | y | = b . Наконец, точка ![]() представляет собой полюс, происходящий от падающей волны:
представляет собой полюс, происходящий от падающей волны:
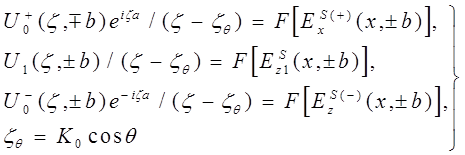 (10)
(10)
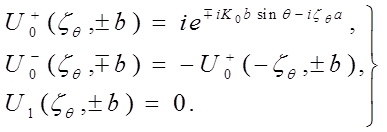 (11)
(11)
Здесь значок справа у неизвестной функции ![]() указывает на то, что в случае значка «+» эта функция регулярна в верхней полуплоскости ( в области U ), а в случае значка « - » рассматриваемая функция регулярна в нижней полуплоскости ( в области L ). В дальнейшем используется этот способ обозначений.
указывает на то, что в случае значка «+» эта функция регулярна в верхней полуплоскости ( в области U ), а в случае значка « - » рассматриваемая функция регулярна в нижней полуплоскости ( в области L ). В дальнейшем используется этот способ обозначений.
С другой стороны, при |y | £b существует разрыв в среде. В результате выполнения прямого преобразования Фурье в волновом уравнении (3) оно превращается в следующие дифференциальные уравнения неодинакового порядка:
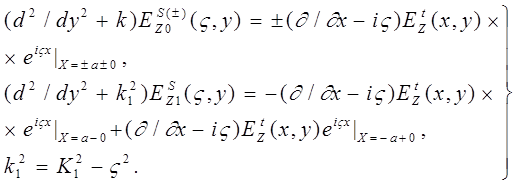 (12)
(12)
Здесь «вынужденные» члены в правых частях можно вывести, принимая во внимание то обстоятельство, что величины в соотношениях (6) и падающая волна (![]() ) непрерывны при | x | = a.
) непрерывны при | x | = a.
Из уравнений (3) следует, что ![]() представляет собой производную
представляет собой производную ![]() , умноженную на постоянный коэффициент, поэтому, полагая
, умноженную на постоянный коэффициент, поэтому, полагая
 (13)
(13)
можем добиться того, чтобы удовлетворялось граничное условие (В3). В приведенных соотношениях символ производной ![]() означает, что в производной
означает, что в производной ![]() выполнен предельный переход
выполнен предельный переход ![]() . Таким образом, разлагая волну на торцевой плоскости ( при | x | = a) в следующий ряд, можем легко найти специальные решения уравнений (12):
. Таким образом, разлагая волну на торцевой плоскости ( при | x | = a) в следующий ряд, можем легко найти специальные решения уравнений (12):
 (14)
(14)
 (15)
(15)
Что касается соотношений (14), то они превращаются в специальный способ разложения в ряд Фурье. Иначе говоря, представляют собой разложения по системе ортогональных функций, превращающихся в нуль при | y | =b. Физически они представляют собой собственные колебания плоскопараллельного волновода. Достаточность таких разложений будет видна из обсуждения свойств регулярности, о которых речь идет ниже. Окончательно, в качестве решения уравнений (12), удовлетворяющих граничным условиям (В2), (В3), можем записать следующие выражения :
 (16
(16
Здесь члены рядов представляют собой частные решения. Кроме того, неизвестные функции, снабженные нижними индексами C , S , представляют собой, с учетом свойств четности в соотношениях (10), следующие выражения ( j=0, 1):
 (17)
(17)
Наконец, выполняются следующие соотношения ( j=0, 1, q= c, s):
![]() (18)
(18)
В заключение обсудим коэффициенты разложений в формулах (14). Как отмечалось и при разъяснении формул (6), выступающих в качестве определений, за исключением членов, связанных с падающей волной (известные выражения), функция ![]() определена при x > a, а функция
определена при x > a, а функция ![]() определена при x <- a. Это означает, что Фурье-компоненты этих функций обладают следующим свойствами регулярности, за исключением полюса при
определена при x <- a. Это означает, что Фурье-компоненты этих функций обладают следующим свойствами регулярности, за исключением полюса при ![]() =
=![]() q: компонента
q: компонента ![]() регулярна в верхней полуплоскости (области U ), а компонента
регулярна в верхней полуплоскости (области U ), а компонента ![]() регулярна в нижней полуплоскости (области L ). С другой стороны, функция
регулярна в нижней полуплоскости (области L ). С другой стороны, функция ![]() определена на ограниченном интервале - a < x < b , так что ее Фурье-компонента представляет собой целую функцию. Конкретно, записывая в следующем виде
определена на ограниченном интервале - a < x < b , так что ее Фурье-компонента представляет собой целую функцию. Конкретно, записывая в следующем виде