Реферат: Модель управления конфликтными потоками в классе алгоритмов

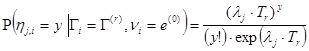; (8.1)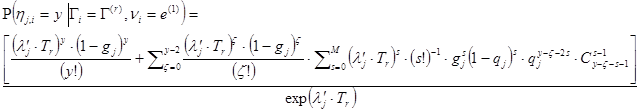 (8.2)

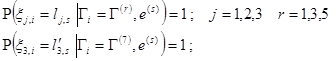(9)

где - целая часть величины , а , - средняя интенсивность обслуживания заявок по потоку если случайная среда на интервале находится в состоянии , здесь - интенсивность пуассоновского поступления заявок по потоку , , 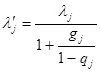, - параметры распределения Бартлетта, - целая часть величины .

6. Марковское свойство компоненты .

Итак, мы определили все компоненты нашей модели: входные потоки, алгоритм управления, потоки насыщения и экстремальную стратегию механизма обслуживания. В соответствии со структурой анализируемой системы управления 3 конфликтными потоками требований, максимальный интерес представляет исследование процессов обслуживания по потокам и . Ключевое свойство дискретной компоненты процесса можно сформулировать в виде следующей теоремы:

Теорема: Последовательности , и при заданном распределении вектора являются марковскими.

Доказательство : Докажем правильность утверждения для последовательности. Сообразно определению, данная последовательность будет марковской, если выполнено равенство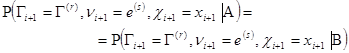

Где

Применяя формулу полной вероятности и принятые в данной модели основные свойства ее случайных элементов, получим:

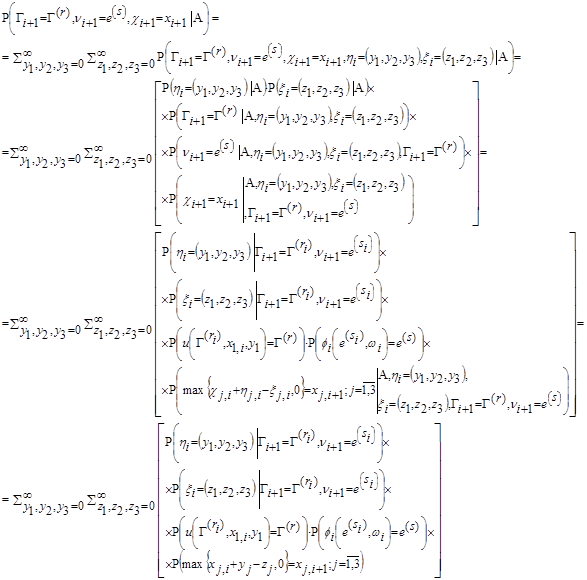
для правой части доказываемого равенства из тех же соображений получим

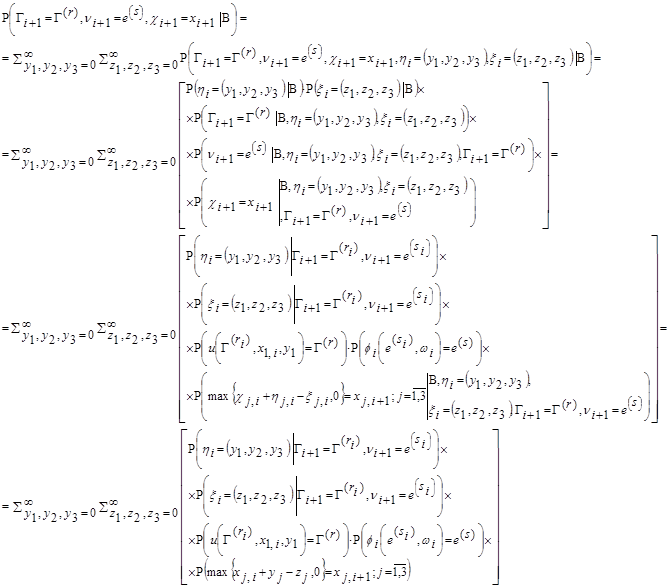
Т.е. доказываемое равенство имеет место. Стало быть, случайная последовательность образует цепь Маркова с бесконечным счетным числом состояний.

Аналогично доказывается марковость последовательностей и .

7. Рекуррентные формулы для одномерных распределений дискретной компоненты маркированного точечного процесса .

Исследуем свойства одномерных распределений

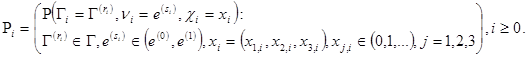
Здесь начальное распределение считается заданным. Получим рекурентные соотношения вида , где - бесконечномерная матрица переходных вероятностей за один шаг процесса . Подробно рассмотрим вероятностные свойства последовательностей и . Из (7) нетрудно получить следующие, реккурентные по соотношения для этих последовательностей:

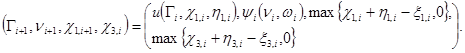
Заметим что исследование последовательностей и , проводятся аналогично.

Введём следующие обозначения: