Реферат: Модель управления конфликтными потоками в классе алгоритмов

(10)

где суммирование ведётся по

Теперь вычислим условные вероятности:

Окончательно формула (10) примет вид:

Здесь суммрование ведётся по всем точкам

Учитывая вид условных распределений для (8.1)-(9), нетрудно получить конкретный вид рекурентных формул для одномерных распределений дискретной компоненты . Подробно приведём только вывод формулы для вероятностей при .

Используя формулу (11), учитывая что при на интервалах времени ни один из потоков не обслуживается, получим для .

где полагаем при .

Вероятности , образуют матрицу

Далее через мыбудем обозначать соответственно целые части величин , где -интенсивность обслуживания по потоку , если случайная среда находится в состоянии .

Поскольку при обслуживаются только требования потока ,

рекуррентные соотношения для вероятностей при получаются в виде:

(13)

(14)

Так как при происходит обслуживание требований только по потоку , то при получим, что при всех и , а при имеем:

(15)

а при любых :

(16)

Наконец для вероятностей имеем при любом , , .

(17)

а при любых , .

(18)

Заметим, что поскольку вероятности для , , то из (12) непосредственно следует, что при всех для , , .

Уточним теперь структуру цепи Маркова . Обозначим через . Сформулируем и докажем два вспомогательных утверждения, касающихся общей структуры цепи и асимптотического поведения распределения рассматриваемой цепи Маркова при .

Лемма 1. Пространство состояний цепи Маркова распадается на незамкнутое множество несущественных состояний и минимально замкнутое множество существенных сообщающихся непериодических состояний.

Доказательство. Из того, что и для всех , следует что случайный процесс за некоторое конечное число шагов из произвольного состояния с положительной вероятностью по цепочке попадёт в состояние . Следовательно состояние является существенным. Согласно теореме 3.5 из /7/ совокупность состояний цепи, сообщающихся с также является существенным. Используя полученные нами рекурентные соотношения (12)-(18) и приведённые выше замечания нетрудно видеть, что множество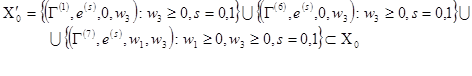

Покажем, что не содержит других состояний, кроме отмеченных. Возьмём, к примеру, состояние где . Тогда по цепочке переходов цепь Маркова перейдёт из существенного состояния в состояние . Следовательно, состояние является существенным и сообщающимся с . Указанный переход возможен с положительной вероятностью, поскольку и . Аналогично доказывается, что возможен переход из или в любое другое состояние, не принадлежащие множеству . Значит . Поскольку состояние достижимо из любого состояния , то множество не является замкнутым, а содержит единственное замкнутое минимальное . Из очевидного неравенства

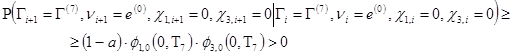
следует, что все состояния из будут непериодическими (/8/ стр. 408). Лемма доказана.

Лемма 2. При любом начальном распределении векторной цепи Маркова либо для всех :

и в системе не существует стационарного распределения, либо существуют пределы:

такие, что , и всистеме существует стационарное распределение.

Доказательство. Из структуры множества и из того, что следует, что векторный случайный процесс из произвольного состояния с положительной вероятностью, не меньшей, чем , за один шаг может достигнуть множества . Обозначим через вероятность того, что рассматриваемая цепь Маркова исходя из произвольного несущественного состояния когда-либо достигнет некоторого существенного состояния из . Известно, что величины , являются решениями системы уравнений вида (8.6), приведённой в /8/ на стр. 392. Тогда, в силу неравенства и леммы 1, эта система является вполне регулярной и имеет ограниченное решение , . В этом можно убедиться непосредсвенной подстановкой. По теореме 11 из /9/ это решение будет единственным. Отсюда на основании эргодической теоремы в главе 15 из /8/ получим утверждение доказываемой леммы.

Итак, ассимптотическое поведение одномерного распределения случайного векторного процесса при не зависит от начального распределения .

Заключение.