Реферат: Модели аналоговых пассивных компонентов программного пакета MicroCAP-7
![]() ФорматсхемМIСROCAP-7:
ФорматсхемМIСROCAP-7:
Атрибут PART: <имя>
Атрибут VALUE: <значение> [IС=<начальный ток>]
Атрибут MODEL: [имя модели]
Атрибут FREQ: [<выражение>] — например 10u*(F/100), при этом значение атрибута FREQ заменяет значение атрибута VALUE при проведении АС-анализа (здесь F — частота), при расчете переходных процессов индуктивность равна значению атрибута VALUE.
Индуктивность, определяемая параметром <значение>, может быть числом или выражением, включающее в себя изменяющиеся во времени переменные, например 100+I(L2)*2. Эти выражения можно использовать только при анализе переходных процессов. В режиме АС эти выражения вычисляется для значений переменных в режиме по постоянному току.
Параметры модели индуктивности приведены в табл. 3.
Таблица 3 Параметры модели индуктивности
| Обозначение | Параметр | Размерность | Значение по умолчанию | ||||
| L | Масштабный множитель индуктивности | — | 1 | ||||
| I L 1 | Линейный коэффициент тока | А–1 | 0 | ||||
| I L 2 | Квадратичный коэффициент тока | А– 2 | 0 | ||||
| ТС1 | Линейный температурный коэффициент индуктивности | °С– 1 | 0 | ||||
| ТС2 | Квадратичный температурный коэффициент индуктивности | °С– 2 | 0 | ||||
| T_MEASURED | Температура измерений | °С | — | ||||
| Т_АВС | Абсолютная температура | °С | — | ||||
| T_REL_GLOBAL | Относительная темпера тура | °С | — | ||||
| T_REL_LOCAL | Разность между температурой устройства и модели-прототипа | °С | — |

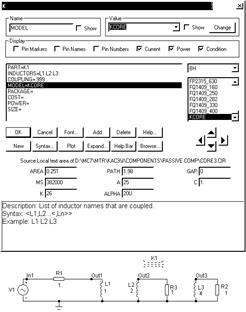
Рис. 3. Окно задания параметров катушки индуктивности
Если в описании опущено <имя модели>, то индуктивность равна параметру <значение> в Генри, в противном случае она определяется выражением
<значение>L(1 +IL1*I+IL2*I2 )[1+TC1(T–TNOM)+TC2(T-TNOM)2 ].
Здесь I — ток через катушку индуктивности при расчете переходных процессов. При расчете частотных характеристик (режим АС) индуктивность считается постоянной величиной, определяемой в рабочей точке по постоянному току.
4. Взаимная индуктивность и магнитный сердечник (К)
Формат схем МС:
Атрибут PART: <имя>
Атрибут INDUCTORS: <имя индуктивности>
Атрибут COUPLING: коэффициент связи>
Атрибут MODEL: [имя модели]
Порядок перечисления имен индуктивностей Lyyy, Lzzz ... безразличен, знак взаимной индуктивности определяется положительными направлениями токов индуктивностей относительно начал обмоток. Параметром взаимной индуктивности является коэффициент связи.
На одном сердечнике помещается одна или несколько обмоток с именами Lyyy, Lzzz... Все обмотки имеют одинаковый <коэффициент связи>. Здесь возможны 2 варианта: а) магнитосвязанными могут быть линейные индуктивности (без сердечника); нелинейные индуктивности с нелинейным магнитным сердечником, определяемым параметрами модели CORE.
a ) Магнитосвязанные линейные индуктивности.
Коэффициент связи Kij двух обмоток (i , j ) определяется выражением:
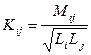
где L i , Lj — индуктивности обмоток; Mij — их взаимная индуктивность. Напряжение на катушке L i , с учетом взаимной индукции определяется выражением:
![]() ,
,
Где Ii — ток втекающий в вывод (+) обмотки (помечен на схеме точкой). В этом случае при вводе в схему связанных индуктивностей посредством вставки элемента K, в открывающемся окне параметров задается лишь позиционное обозначение сердечника KN, позиционные обозначения всех катушек индуктивности (INDUCTORS) с которыми он связан и коэффициент связи (COUPLING) (см. рис. 4., а). Имя модели сердечника при этом не вводится.
б) Магнитосвязанные катушки с нелинейным магнитным сердечником. При описании каждой обмотки Lyyy..., упомянутой в составе сердечника в позиции INDUCTORS, изменяется смысл параметра <значение>. Т.е. численное значение, задаваемое в позиции VALUE окна параметров катушки индуктивности теперь определяет не индуктивность, а число витков соответствующей обмотки сердечника. В этом случае в позиции MODEL окна параметров сердечника K вводится имя модели нелинейного магнитного сердечника (возможно из открывающегося в этом же окне списка, см. рис. 4., б). Модель магнитного сердечника представляет собой вариант модели Джилса-Атертона, в котором безгистерезисная кривая намагниченности ферромагнетика является гиперболической функцией напряженности магнитного поля H (coth).