Реферат: Модели и методы адаптивного контроля знаний

(1)

где I – оценка за контрольную работу; {c₁ , c₂ , …, c_м } – вектор граничных значений; M – максимальная возможная оценка (например, при пятибалльной шкале M = 5).

Методы оценивания в основном используются на втором и третьем этапе, хотя существует ряд методов, которые применяются для выставления оценки только на последнем этапе.

Методы оценки знаний можно разделить на два основных класса (рис. 5):

математические методы;

классификационные методы.

К математическим моделям оценки знаний относятся:

Простейшая модель. Данная модель является самой простой и самой распространенной. Ответ студента на каждое задание оценивается по двухбалльной (правильно или неправильно) или многобалльной (например, пятибалльной) шкале. Оценка выставляется путем вычисления значенияR:

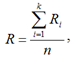
где R_i - правильный ответ обучаемого на i -е задание; k – количество правильных ответов из n предложенных (k n), которое затем обычно округляется по правилам математики. К достоинствам данной модели следует отнести простоту ее реализации. Недостатком модели является ее зависимость от единственного параметра (количества правильных ответов), т.е. она не учитывает не полностью точные ответы и характеристики заданий. Простейшая модель имеет самую низкую надежность, т.к. не позволяет объективно оценить знания студента.

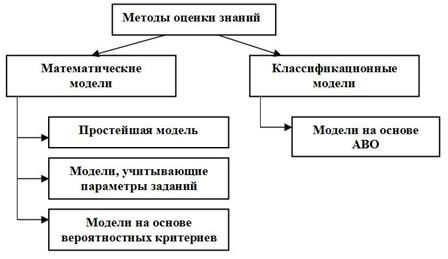
Рис. 5. Модели и методы оценки знаний.

Модели, учитывающие параметры заданий. В этих моделях при выставлении оценки используются характеристики контрольных вопросов. Существуют различные модификации данного типа моделей.

Модель, учитывающая время выполнения задания и/или общее время контрольной работы. Для правильных ответов рассчитывается значение R_i по формуле:

,

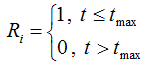где t – время выполнения задания; t_max – время, отведенное для выполнения задания.

Далее итоговая оценка вычисляется аналогично “Простейшей модели”.

Модель на основе уровней усвоения. В этой модели характеристикой задания является уровень усвоения, для проверки которого оно предназначено. Таким образом, задания разделяются на пять групп, соответствующих уровням усвоения: понимание, опознание, воспроизведение, применение, творческая деятельность [Соловов, 1995]. Для каждого задания определяется набор существенных операций. Под существенными понимают те операции, которые выполняются на проверяемом уровне. Операции, принадлежащие к более низким уровням, в число существенных не входят. Для выставления оценки используется коэффициент К_a :

где Р₁ - количество правильно выполненных существенных операций в процессе контроля;

Р₂ - общее количество существенных операций в контрольной работе;

a = 0, 1, 2, 3, 4 – соответствуют уровням усвоения.

Оценка выставляется на основе заданных граничных значений по соотношениям:

Кa < 0.7	– неудовлетворительно;
0.7 Кa < 0.8	– удовлетворительно;
0.8 Кa < 0.9	– хорошо;
Кa 0.9	– отлично.

Данная модель используется в системе КАДИС [Соловов, 2002].

Метод линейно - кусочной аппроксимации [Зайцева, 1989; Зайцева, 1991]. Алгоритм оценивания основан на классификации заданий (вопросов) по их дидактическим характеристикам (значимость (z), трудность (d), спецификация (s)). Число баллов, полученных студентом за выполнение n заданий, определяется по формуле:

,

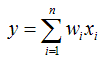где x_i – оценка за выполнение i–го задания;

n – число заданий;

W = {w₁ ,w₂ ,…,w₃₆ } – вектор весовых коэффициентов заданий, зависящий от их дидактических характеристик.