Реферат: Модели и методы адаптивного контроля знаний
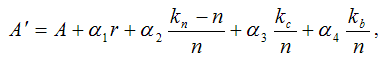
где r – ранг обучаемого (1, 2, или 3);
kn – количество попыток выполнения n заданий;
kc – количество обращений к справочной информации;
kb – количество заданий, выполненных с превышением отведенного времени (kb 
n);
a1 , a2 , a3 , a4 - коэффициенты.
Далее оценка выставляется по формуле (1). Аналогичным образом определяется и уровень усвоения (ранг) студента. Преимущество данной модели: использование как четырех дидактических характеристик заданий, так и уровня подготовленности (ранга) из модели студента, что позволяет повысить надежность результатов контроля. Модель в качестве основной использовалась в семействе АОС, разработанных в РТУ.
Модели на основе вероятностных критериев. Главным в данных математических моделях контроля знаний являются утверждения о зависимости вероятности правильного ответа студента от уровня его подготовленности и от параметров задания [Rasch, 1977; Lord, 1980; Аванесов, 1998]. Суть этих моделей состоит в том, что на основе известных априорных вероятностей рассчитываются апостериорные вероятности Р (Hi ) гипотезыHi , что студент заслуживает оценку i. При вычислении вероятности Р(Hi ) учитываются: сложность и время выполнения заданий; число предложенных обучаемому заданий; число неправильно выполненных заданий и др. Рассчитанные вероятности анализируются и/или сравниваются с граничными значениями, учитывая риски недооценки и переоценки выставления оценки i. Если полученные результаты однозначно позволяют выставить оценку, то контроль, как правило, завершается. В противном случае студенту выдается очередное задание. Модель данного типа использовалась в АОС ВУЗ [Волков, 1984], различные модификации модели успешно применяются и в настоящее время [Попов, 2000; Моисеев, 2001].
Основная идея классификационных моделей заключается в отнесении студента к одному из устойчивых классов с учетом совокупности признаков, определяющих данного студента. При этом используется специальная процедура вычисления степени похожести (оценки) распознаваемой строки (совокупности признаков обучаемого) на строки, принадлежность которых к классам заранее известна.
Алгоритм, основанный на вычислении оценок (АВО) был впервые предложен Ю.И. Журавлевым [Журавлев, 1978] и позднее использовался для классификации обучаемых по уровням полготовленности [Зайцева, 1989] и для оценки знаний в качестве дополнительного метода в обучающих системах РТУ [Зайцева, 1989а[. Данная модель предусматривает построение таблицы обучения То nm , в которой каждая строка представляет собой набор признаков обучаемого характеризующих работу студента в процессе КЗ: количество предложенных заданий (n), средний балл (A), количество попыток выполнения заданий (kn ), количество обращений к справочной информации (kc ), ранг (r). При выставлении оценки вычисляется степень похожести совокупности признаков конкретного студента I(S) = {
1 , 2 , …, m } на строки, входящие в таблицу обучения То nm , на основании чего осуществляется отнесение его к определенному классу Kj . Для этого вычисляется число строк каждого класса Kj , близких по выбранному критерию классифицируемому объекту S. Строка таблицы обучения То nm I(Sj i ) = {a j i1 , …, aj im } и распознаваемая строка I (S) = {1 , 2 , …, m } считаются похожими, если выполняются неравенства |aj ik –k | 
, где (k =1, …, m) - точность сравнения. Студент относится к классу Kj , имеющему максимальную оценку max Гj (S, Kj ), j = 1, …, m. Данная модель в настоящее время применяется в системе [КИОС, 1992] с единственным отличием: вместо одной таблицы обучения, содержащей данные для различных классов, в КИОС используются четыре таблицы обучения для классов “отлично”, “хорошо”, “удовлетворительно” и “неудовлетворительно”, названные эталонными таблицами оценивания.
Таким образом, для оценивания знаний студентов применяются разные модели и алгоритмы, начиная с самых простых, учитывающих лишь процент правильно выполненых заданий при двухбалльной системе оценки отдельного вопроса, и заканчивая сложными составными, в которых используются всевозможные параметры контроля и многобалльная система оценки как отдельных заданий, так и работы в целом [Прокофьева, 2001; Прокофьева, 2002]. В таблице 2 приведены рассмотренные выше модели и методы оценки знаний и используемые параметры. Все методы оценивания предусматривают в процессе КЗ сбор данных о ходе контроля (в таблице 2 эти параметры подчеркнуты, остальные определяются на этапе обучения и могут быть изменены преподавателем перед началом КЗ). Метод линейно - кусочной аппроксимации и модели на основе вероятностных критериев предполагают также вычисление некоторых функций, которые обычно используются для определения дальнейшего хода контроля.
Заключение
Методы проведения контроля и методы оценивания тесно взаимосвязаны. В общем случае любая модель выставления оценки может быть использована при любом методе проведения КЗ, за исключением моделей на основе вероятностных критериев, которые предназначены лишь для частично адаптивных и адаптивных методов организации контроля. С другой стороны, простейшую модель выставления оценки и модель, учитывающую время ответов, целесообразно применять только совместно с неадаптивными методами КЗ. Таким образом, при адаптивном контроле знаний рекомендуется использовать модели на основе вероятностных критериев, АВО или уровней усвоения, а также метод линейно - кусочной аппроксимации. По нашему мнению, в современные адаптивные системы обучения и контроля знаний следует включать несколько различных методов и моделей, чтобы преподаватель имел возможность выбрать метод проведения контроля и модель выставления оценки, отвечающие целям контроля и наиболее подходящие для отдельного или группы студентов.
Таблица 2. Модели оценивания и используемые параметры.
| Модели оценки знаний | Используемые данные | ||
| Параметры задания | Параметры КЗ | ||
| 1 | Простейшая модель | – | Число заданий; число правильных ответов |
| 2 | Модель, учитывающая время ответов | – | Число заданий; число правильно выполненных заданий без превышения отведенного времени |
| 3 | Модель на основе уровней усвоения |
Уровень усвоения УМ; трудность и сложность УМ | Число правильно выполненных существенных операций; общее число существенных операций в заданиях |
| 4 | Метод линейно - кусочной аппроксимации | Значимость, трудность, спецификация | Число заданий; число попыток выполнения заданий; число обращений к справке; число заданий, выполненных с превышением отведенного времени; граничные значения |
| 5 | Модели на основе вероятностных критериев | Сложность | Число заданий; время ответа; априорная вероятность получения оценки; граничные значения; риски недооценки и переоценки |
| 6 | Модели на основе АВО | - | Число заданий; число попыток; число обращений к справке; точность сравнения |
Список литературы
[Аванесов, 1998] Аванесов B.C. Композиция тестовых заданий. - М.: Адепт, 1998. – 217 с.
[Алексеенко, 1978] Алексеенко Е. А., Довгялло А. М., Косая И. Х. СПОК – система программирования и поддержания обслуживающих и обучающих курсов // Управляющие системы и машины. – 1978. – №2. – с. 127 – 128.
[Андреев, 2002] Андреев А.Б., Акимов А.В., Усачев Ю.Е. Экспертная система анализа знаний ”Эксперт-ТС” // Proceedings. IEEE International Conference on Advanced Learning Technologies (ICALT 2002). 9-12 September 2002. Kazan, Tatrstan, Russia, 2002, – p. 97 - 101.
[Артемов, 1999] Артемов А., Павлова Н., Сидорова Т. Модульно-рейтинговая система // Высшее образование в России. – 1999. –№4. –с. 121 – 125.
[Беспалько, 1977] Беспалько В.П. Основы теории педагогических систем. Проблемы и методы психолого-педагогического обеспечения технических обучающих систем. – Воронеж : Воронежск. ун-т, 1977. – 304 с.
[Беспалько, 1989] Беспалько В. П. Слагаемые педагогической технологии. – М.: Педагогика, 1989. – 192 с.
[Волков, 1984] Волков С.З. Алгоритм управления контролем знаний // Кибернетика и исследование операций в управлении учебным процессом: Тез. докл. – Рига: РПИ, 1984, – с. 67 – 70.
[Гладковский, 1997] Гладковский В.И., Гладыщук А.А., Панасюк И.М. Воспитательные функции рейтинговой системы оценки знаний (РСОЗ) // Высшая школа: состояние и перспективы. – Минск: РИВШ БГУ, 1997. – 107 с.
[Журавлев, 1978] Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания и классификации // Проблемы кибернетики. – 1978. – Вып. 33. – с. 5 –68.
[Зайцева, 1982] Автоматизированная обучающая система КОНТАКТ/ОС / Л.В. Зайцева, Л.В. Ницецкий, Л.П. Новицкий и др. – М.: Моск. науч.– учеб. центр СНПО “Алгоритм”, 1982. – 108 с.
[Зайцева, 1989] Зайцева Л.В., Новицкий Л.П., Грибкова В.А. Разработка и применение автоматизированных обучающих систем на базе ЭВМ. – Под ред. Л.В.Ницецкого. – Рига : “Зинатне”, 1989. – 174 с.
[Зайцева, 1989а] Зайцева Л.В., Новицкий Л.П., Прокофьева Н.О. Контроль знаний обучаемых с помощью методов линейно-кусочной аппроксимации и вычисления оценок // Методы и средства кибирнетики в упр. учеб. проц. высш. шк. – Рига: Рижск. политехн. ин-т, 1989, – с. 39 – 48.
[Зайцева, 1991] Зайцева Л.В. Методы контроля знаний при автоматизированном обучении. - Автоматика и вычислительная техника, 1991, Nr 4, с. 88 – 92.
[Зайцева, 2000] Зайцева Л.В. Некоторые аспекты контроля знаний в дистанционном обучении // Сборник научных трудов 4-й международной конференции ”Образование и виртуальность – 2000” – Харьков – Севастополь : УАДО, 2000, - с. 126 – 131.