Реферат: Моделі мультиграничної сегментації зображень

Твердження 1. Класи толерантності утворюють правильне покриття множини .

Довільне покриття скінченної множини названо впорядковано зв’язним, якщо існує індексація, при якій у будь-якому представнику покриття втримуються тільки занумеровані підряд (без пропусків) елементи, тобто , , . Довільна трійка різних елементів множини із заданим на ній покриттям названа транзитивним триплетом, якщо будь-яка пара точок лежить хоча б у одному елементі покриття.

У загальному випадку будь-яка пара аналогічно (1) індукує на множині відношення толерантності, а саме

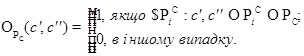
Вивчені властивості правильних і впорядковано зв’язних покриттів.

Властивість 1. Для будь-якої пари елементів впорядковано зв’язного, правильного покриття існує хоча б один нетранзитивний триплет, який належить до їхнього об’єднання , два елемента якого не належать одному елементу покриття, тобто

.

Властивість 2. Якщо для будь-якої пари елементів довільного покриття існує нетранзитивний триплет , який лежить у їхньому об’єднанні, то це покриття правильне.

Властивість 3. Довільне розбиття скінченної множини є впорядковано зв’язним покриттям.

Довільне бінарне відношення , яке задане на множині , названо функціональним, якщо задана деяка функція , а на задано покриття і , де , .

Твердження 2. Функціональне відношення не зміниться, якщо з покриття, що його індукує, будуть вилучені всі неправильні елементи.

Ці результати створили передумови для вивчення питань взаємозв’язку завдання покриттів значень функцій розподілу яскравості і результатів сегментації.

На питання, коли суміжні класи і класи толерантності збігаються для функціональних відносин, відповідь дає

Твердження 3. Класи образів і прообразів заданого на довільній множині функціонального відношення , індукованого функцією і деяким упорядковано зв’язним покриттям , є класами толерантності тоді і тільки тоді, коли – розбиття.

Інтерпретація доведеного твердження прозора – при раціональному розбитті діапазону зміни функції розподілу яскравості можна одержати "області подібності" на носії зображення у вигляді класів толерантності, які трактуються доволі просто.

Використання впорядкованого зв’язного покриття є принциповим, тобто якщо його виключити із розгляду, то збіг класів образів і класів толерантності не гарантує, що є розбиттям.

На питання про зв’язок класів толерантності й суміжних класів відповідає

Твердження 4. Будь-який суміжний клас довільного толерантного відношення містить підмножину – клас толерантності, якому належить елемент, що породжує цей суміжний клас.

Побудова обчислювальних моделей базується на такому результаті.

Твердження 5. Якщо матриця довільного толерантного відношення має блочний вигляд, то покриття і , які утворені відповідно суміжними і толерантними класами, є впорядковано зв’язними. При цьому – правильне покриття, а – правильне тоді і тільки тоді, коли суміжні класи або класи толерантності не перетинаються для елементів, які мають різні образи, і фактично збігаються.

Будь-яка функціональна толерантність, яка індукована відображенням , яке можна трактувати як зображення, тобто функцією розподілу яскравості у полі зору, ставить у відповідність кожному елементу покриття бінарні відношення на множині

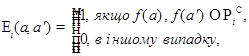
де , , , .

Оскільки відображення є відображенням у множині , довільний елемент має повний прообраз – так називані лінії рівня . Якщо розглянути при відображенні всіх елементів покриття , то по кожному фіксованому елементу покриття отримаємо об’єднання всіх ліній рівня його елементів, тобто

.

Це відношення є відношенням еквівалентності, продукуючи клас еквівалентності правилом

. (2)

Відзначимо, що класи є передкласами толерантності, оскільки складаються із парних толерантних елементів. Система передкласів , яка індукована еквівалентностями (правилом (2), буде в просторі функціональної толерантності базисом, тобто відповідати умовам