Реферат: Моделі мультиграничної сегментації зображень

Спільна обробка покриттів, отриманих різними шляхами, дозволяє отримати додаткову інформацію для побудови розбиттів, що найточніше відповідають об’єктам, які шукаються. Отримані результати являють собою основу для введення операцій між покриттями і критеріїв переходу до розбиттів, адекватних структурі сцен, що спостерігаються.

Третій розділ. Після одержання часткової сегментації зображень головним завданням стає трансформація класів еквівалентності або толерантності для забезпечення передумов тематичної інтерпретації візуальної інформації. У розділі запропоновано методи перетворень розбиттів і покриттів поля зору.

Сегментовані зображення представлені у вигляді , де , при аналізі розбиття і під час обробки покриття. Внаслідок сегментації класи еквівалентності або толерантності розмічені, тобто існує індексуюче відображення таке, що . Розглянуто операції, що відповідають умовам

, (3)

, (4)

, (5)

. (6)

Умова (3) вказує на існування необхідного відображення. Умова адитивності (4) разом з умовою монотонності (5) гарантує можливість пофрагментної обробки. Умова (6) забезпечує обробку декількох множин, що визначають сегментоване зображення. Якщо відображення взаємно однозначне, то включення (6) переходить у рівність. Як другий операнд можуть використовуватися або елементи множини , або інші результати сегментації , або деякі фіксовані множини , які передбачають акцентування або фільтрацію тих або інших властивостей. На сегментованих зображеннях виділені межі окремих областей , а також їхні внутрішні частини .

Для маніпуляцій з розбиттями (покриттями) як базові обрані операції алгебри Мінковського на площині. По-перше, результати сегментації є замкнутими щодо операцій алгебри Мінковського, по-друге, додавання і віднімання Мінковського, де операнди – довільні множини, що задовольняють умовам (3) – (6).

Якщо фіксувати просторову форму й структуру однієї з множин, то можна одержувати підмножини із заданими властивостями (стосовно обробки результатів сегментації одержуємо бінарну морфологію).

Як базові операції використані операції бінарної морфології: і – розширення і звуження відповідно. Тут – множина, яка фіксується і має назву структурний елемент, .

Часто при трансформаціях розбиттів або покриттів корисними виявляються операції визначення внутрішніх частин і замикання , оскільки: багаторазове використання одних і тих самих операцій і не міняє результату; завжди ; операція видаляє дрібні об’єкти і тонкі частини великих об’єктів, приводить до розділення об’єктів, які з’єднані тонкими лініями, тобто реалізує деякі елементарні алгоритми фільтрації; операція заповнює мілкі отвори в об’єктах, об’єднує найближчі об’єкти, тобто при відповідному виборі прототипів аналіз багатозв’язних об’єктів можна зводити до обробки однозв’язних областей.

Якщо використовувати і як структурні елементи, отримуємо ортогональні () або ізотропні () межі. Застосовуючи розклад чотиризв’язності , де , , отримуємо горизонтальні та вертикальні складові межі.

Маніпуляції із сегментованими зображеннями (об’єднання розбиттів із метою огрублення областей інтересу, їхнє перетинання для підвищення ступеня деталізації й т. ін.) можуть дозволити знаходити розумний компроміс між надмірною і недостатньою сегментацією. Для визначення операцій із сегментованими зображеннями введемо характеристичну функцію класу еквівалентності

Необхідно вказати граничні умови , і своєрідну подвійність введених відношень .

У розділі встановлений взаємозв’язок між парами і елементів двох довільних розбиттів і

,

,

.

Для отримання розбиттів, що відповідають контексту реальних сцен, для операцій типу злиття-розщеплення потрібне одночасне використання декількох класів еквівалентності. Показано, що для

,

.

Якщо ввести позначення , де означає внутрішню частину елемента з межею і визначити відношення

то матриця однозначно задає всі можливі варіанти взаємного розташування елементів розбиття, аналіз яких підвищує точність і надійність інтерпретації сегментованих зображень. Використання індикаторної функції

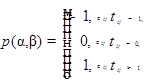
дозволяє для будь-яких розбиттів ,визначити

, ,