Реферат: Моделювання розробки та прийняття рішень

Надмірна вартість. Вигоди від використовування моделі, як і інших методів управління, повинні з лишком виправдовувати її вартість. При встановленні витрат на моделювання керівництву слід враховувати витрати часу керівників вищого і нижчого рівнів на побудову моделі і збір інформації, витрати і час на навчання, вартість обробки і зберігання інформації.

5. Поняття програми, програмованих та непрограмованих рішень

Програмовані рішення – це ті, що повторюються багатократно і мають напрацьовані правила й процедури прийняття.

Непрограмовані рішення – це ті, що виниклу проблему мають вирішувати вперше, отже, всі етапи підготовки рішення треба розробляти спеціально.

Програма - це деталізована послідовність дій, що має деяку мету або завдання і відповідає на реакцію системи та зовнішнього середовища.

Відповідно, програмовані рішення - це гранично деталізована послідовність дій в суворо певних ситуаціях.

Переваги такого підходу очевидні: знижується вірогідність помилки, зменшується час на ухвалення рішення, з виконавця знімається відповідальність.

Проте зрозуміло, що подібний точний алгоритм годиться лише для суворо певної ситуації. Отже, її невірна ідентифікація може призвести до великих втрат. Крім того, в деяких ситуаціях, з часом така схема може стати неефективною або навіть помилковою. Крім всього іншого жорстка регламентація діяльності робить роботу виконавців нецікавою, позбавляє їх ініціативи і знижує увагу. Як правило, чим вищий рівень управління, на якому приймається рішення, і чим більше їх важливість, тим менше частка програмованих рішень.

Непрограмовані рішення використовуються в якісно нових, нестандартних, складних ситуаціях, пов'язаних з дією невідомих чинників.

6. Моделі лінійного та нелінійного програмування

Моделі лінійного програмування застосовують для знаходження оптимального рішення в ситуації розподілу дефіцитних ресурсів за наявності конкуруючих потреб. Наприклад, за допомогою моделі лінійного програмування керівник виробництвом може визначити оптимальну виробничу програму, тобто розрахувати, яку кількість виробів кожного найменування слід проводити для отримання найбільшого прибутку при відомих об'ємах матеріалів і деталей, фонді часу роботи устаткування і рентабельності кожного типу виробу. Велика частина розроблених для практичного застосування оптимізаційних моделей зводиться до завдань лінійного програмування.

Максимізуюча (мінімізуюча) функція являє собою прийнятий критерій ефективності вирішення завдань, що відповідає поставленій меті, та називається цільовою функцією.

Обмеження характеризують наявні можливості вирішеня завдання.

Суть розв'язання завдань лінійного програмування полягає в знаходженні умов, що спрямовують цільову функцію в мінімум чи максимум.

Рішення, що задовольняє умови завдання і відповідає поставленій меті, називається оптимальним планом.

Якщо кількість змінних системи обмежень і цільової функції в математичній моделі завдання лінійного програмування дорівнює двом або трьом, то таке завдання можна вирішити графічно чи аналітично. При більшій кількості змінних завдання вирішують, як правило, аналітичним шляхом.

З урахуванням характеру аналізованих операцій і форм залежності чинників, що склалися, можуть застосовуватися і моделі інших типів: при нелінійних формах залежності результату операції від основних чинників – моделі нелінійного програмування; при необхідності включення в аналіз чинника часу – моделі динамічного програмування; при імовірнісному впливі чинників на результат операції – моделі математичної статистики (кореляційно-регресійний аналіз).

Умови завдання подаються за допомогою системи лінійних рівнянь чи нерівностей, що виражають обмеження, які накладаються на використання наявних ресурсів:

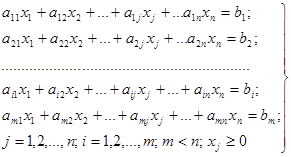, (1)

де х_j – шукані величини, що містять розв'язання поставленого завдання;

а_ij та b_i – відомі постійні величини, що характеризують умови завдання.

Цільова функція (лінійна форма) надається у вигляді:

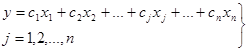, (2)

де с_j — постійні коефіцієнти (коефіцієнти вартості).

Умови завдання (обмеження) можуть бути надані також у вигляді нерівностей.

Геометрична інтерпретація завдання лінійного програмування можлива лише при наявності двох незалежних змінних. При трьох змінних наочне уявлення істотно ускладнюється, так як у цьому випадку має місце деякий випуклий багатогранник в трьохвимірному просторі, що відповідає об'єму допустимих планів.

При кількості змінних більше трьох завдання втрачає геометричну наочність, так як важко уявити собі, наприклад, чотирьохвимірний простір. Проте ідея одержання рішення, розглянутого вище, зберігає зміст і для випадку багатовимірного простору.

На основі такої ідеї створений і розроблений один з основних методів вирішення завдань лінійного програмування — так званий симплекс-метод.

Симплекс-метод – алгебраїчна форма вирішення завдання лінійного програмування. При обґрунтуванні симплекс-методу звертаються до двохвимірного випадку, що дозволяє досить просто перейти від геометричного уявлення до його алгебраїчної аналогії.

У моделях нелінійного програмування цільова функція чи хоча б одне з обмежень нелінійні (тобто на графіках зображуються непрямими — кривими лініями).

Умови завдання надаються за допомогою системи нелінійних рівнянь чи нерівностей, що виражають обмеження, накладені на використання наявних ресурсів: