Реферат: Нахождение кратчайшего маршрута между двумя городами по существующей сети дорог

нахождение кратчайшего маршрута между городами по сети дорог;

определение максимальной пропускной способности при транспортировки нефти;

составление временных графиков работ и др.

Существуют три наиболее эффективных алгоритма нахождения кратчайшего пути:

1) алгоритм построения минимального основного дерева. Предполагает соединение всех узлов сети с помощью путей наименьшей длины.

2) алгоритм Дейкстры. Используется для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети

3) алгоритм Флойда. Используется для нахождения оптимального маршрута между любыми двумя узлами сети.

Основные определения

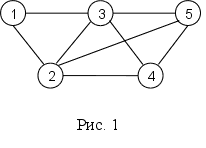
Сеть состоит из множества улов, связанных дугами (или ребрами). Таким образом, сеть описывается парой множеств (N,A), где N – множество узлов, а A – множество ребер. Например, сеть, показанная на рис. 1, описывается след образом.

N = {1, 2, 3, 4, 5},

A = {(1, 3), (1, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}.

С каждым типом сети связан определенный тип потоков (например, транспортный поток нефти в нефтепроводах или автомобильные потоки в сети дорог). В общем случае потоки в сети ограничены пропускной способностью ее ребер, которая может быть как конечной, так и бесконечной.

Ребро называется направленным, или ориентированным (и в этом случае ребро будем называть дугой), если в одном направлении возможен только положительный поток, а в противоположном – только нулевой. В ориентированной сети все ребра ориентированы.

Путем называется последовательность различных ребер, соединяющих два узла, независимо от направления от направления потока в каждом ребре. Путь формирует цикл, если начальный и конечный узлы совпадают. Например, на рис. 2 ребра (2, 3), (3, 4) и (4, 2) составляют цикл. Ориентированный цикл – это цикл, в котором все дуги ориентированы в определенном направлении.

Связная сеть – такая сеть, у которой любые два узла связаны по крайней мере одним путем. На рис. 1 показан именно такой тип сети и не имеющий циклов. Остовное дерево – это дерево, содержащая все узлы сети. На рис. 2 показаны дерево и Остовное дерево для сети из рис. 1.

2. Математическая формулировка задачи, обоснование

Алгоритм Флойда

Алгоритм Флойда находит кратчайший путь между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i ,j) равен расстоянию d_ij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i ,j), и равен бесконечности в противном случае.

Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 3). Если выполняется неравенство d_ij + d_jk < d_ik, то целесообразно заменить путь i → k путем i → j → k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

Алгоритм Флойда требует выполнения следующих действий.

Шаг 0. Определяем начальную матрицу расстояний D₀ и матрицу последовательности

узлов S₀. Диагональные элементы обеих матриц помечаются знаком “ – “,

показывающим, что эти элементы в вычислениях не участвуют. Полагаем k=1.

Основной шаг. Задаем строку k и столбец k как ведущую строку и ведущий столбец.

Рассматриваем возможность применения треугольного оператора ко всем элементам d_ij матрицы D_k-1. Если выполняется неравенство

d_ij + d_jk < d_ik (i ≠k, j≠k, i ≠j),