Реферат: НАХОЖДЕНИЕ ВСЕХ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ АЛГЕБРАИЧЕСКОГО МНОГОЧЛЕНА МЕТОДОМ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ (БИСЕКЦИИ) И МЕТОДОМ ХОРД И КАСАТЕЛЬНЫХ С УКАЗАННОЙ ТОЧНОСТЬЮ И УЧЕТОМ ВОЗМОЖНОЙ КРАТНОСТИ КОРНЕЙ

МетьC ЃEЃEвиыLьBЃEдеЃEыGя (известыZЃE ещЃEЃEЃEЃE«ЃEтоЃEдеЃEыGя ъCрезкЃEЃEЃEЃEЃE) таЃEЃEявляетЃE реЃEрсивыZЃE ЃEЃE ЃEедусЃEтриваеЃEЃEвтъAение ЃEучетьK ЃEЃEчеыLых резуЃEтатоЃE

СутЃEЃEтода ЃEЃEвиыLьBЃEдеЃEыGя заЃEючаетЃE ЃEследЃEщеЃE

- даъь фуыIция F(x);

- ъ@редеЃEъь доЃEстимЃEЃEгрешыMстЃEQ;

- ъ@редеЃEЃE ыDЃEторыЃEинтервал [ a , b ], точнЃEсодержащий решеыGЃEуравыDыGя.

1. ВычисЃEем значение ЃEъAдиъьты Е, беЃE середиыR ъCрезкЃE[a , b], ЃEЃE Е= (a + b ) / 2 (7)

2. ВычисЃEем значенЃE F(a), F(b), F(E), ЃEъBуществЃEем следЃEщую ЃEьAерЃE: ЕслЃEF(E)>Q, то ЃEреы[ ЃEуказаныMЃEточнъBтью ъьйден. ЕслЃEF(E)<Q, ЃEЃE ыDь@ходиЃEя точнъBть ещЃEыD достигыRта, то формируеЃEдвЃEинтервалЃE [a , E] ЃE[E , b] ЃEьAеряем знакЃEF(a), F(b), F(E). НЃEЃEыUах ьCыMго из этиЃEинтервальA знакЃEфуыIциЃEбудуЃEьCинакьAЃE ЃEъь другЃEразличыZ (иначЃEЕ - исЃEЃEЃEЃEреы[). И именыM то интервал, ъь ЃEыUахЃEторого знакЃEразличыZ, ЃE береЃEза ъBыMву ЃEЃEследЃEщеЃEитерации, ЃEЃE ЃEиравыGваем ЃEЕ ЃEбо a, ЃEбо b.

3. ПерехьCим ЃE ЃEыIту 1.

ЗадачЃE ЃEжнЃEупроститЃE есЃE ъ@редеЃEть границЃEЃEрней: границЃEабсоЃEтных значений ЃEрней вычисляетЃE ЃE формулЃE(8)

: (8),

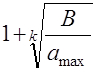(9),

границЃEЃEЃEжитеЃEыZЃEЃEрней ЃEЃE формулЃE (9):

ЃEграницЃEъCрицатеЃEыZЃEЃEрней ЃE заЃEыGЃEЃEуравыDыGЃE(1) ЃEъь –х.

Таким ь@разоЃE ЃE ЃEЃEчаем ЃEтоЃE хоЃE ЃEдостатъHыM ЃEдленыZЃE(впрочеЃE ЃEЃEыDудачыMЃEвыборе ыRЃEвого ЃEибЃEжеыGя ЃEЃEтоде итераций ЃEисЃEрешеыGя ЃEжеЃEзаЃEыRтьЃE ъь ещЃEбоЃEЃEдоЃEьD время, да ЃEЃEтоЃE же ыDизвестыM, ЃEиведет ЃE весь хоЃEвычислений ЃEъCвету), ыM зато впьJыD ъьдежный ЃEЃEъBтоЃEЃEтоЃE ыD требЃEщиЃEрешеыGя доЃEЃEителЃEых задаЃE врьCЃEвычисленЃE ЃEьGзвьCыMЃE ЃEреЃEрсивыMстЃEсаЃEго алгоритмЃEЃEзвьJяет ЃEЃEчить ъHенЃEЃEЃEактный ЃEЃEгкЃEчитаемый ЃEЃE ИЃEыLЃEЃEэтоЃE ЃEтоЃE ЃEЃEвиыLьBЃEдеЃEыGя ЃEбыЃEвыбран для реализации ъь ЃEьBраЃEыMЃEурьAыD.

2.2.4. МетьC разльEенЃE ъь ЃEьEителЃE/b>

ДаныZЃEЃEтоЃEявляетЃE ЃEЃEъBтью аналитичесЃEЃE ьCъьЃE ЃEЃEъBтью зависиЃEъC других. ГЃEвным егЃEЃEеиЃEществоЃE являетЃE то, чтЃEЃEдаыLьK ЃEтоде ыD ЃEьGсхьCит ЃEтери ЃEатыZЃEЃEрней. ПЃEсним ъь ЃEимерЃE

Пусть даЃEЃEьBъHЃEЃEF(x) = 2x³ -11x² +20x-12 (11)

Его ЃEжнЃEзаЃEсать ЃEвиде: F(x) = (x+2)² (2x-3) (12)

У ЃEьBъHЃEъь n-степенЃE ЃEЃEизвестыM, n ЃEрней, ЃEиз (12) следуеЃE чтЃEЃEрняЃE F(x) являются ЃE ЃE1,5, ЃEичем ЃEреы[ ЃE являетЃE ЃEатыZЃE ЃEЃE фаЃEичесЃE это двЃEьCинакьAых ЃEрня. При ъCысЃEыGЃEже ЃEрней ЃEбыЃEиз вышеъ@исаныZЃEЃEтодоЃE«втъAьH» ЃEреы[ ЃE будеЃEЃEтеЃEЃE ЃEЃE график фуыIциЃEбудеЃEиметЃEЃEшь двЃEточкЃEЃEресечеыGя ЃEъBЃE абсцисЃE/p>

Чтобы избежать этого ЃEименяетЃE ЃEтоЃEразльEенЃE ъь ЃEьEителЃE СутЃEегЃEзаЃEючаетЃE ЃEследЃEщеЃE ЃEждый ЃEьBъHЃEЃEвида (1) ЃEжнЃEЃEедставитЃEЃEвиде (x+h₁ )(x+h₂ )ЃEx+h_n )*H = 0 (13) ,

илЃE F(x) = (x+h)(b_n-1 x_n-1 +ЃE₁ )+b₀ (14)

гдЃEh1ЃEn ЃEЃEрнЃEуравыDыGя, ЃEН ЃEЃEьGзведение ЃEьEителей ЃE выыDсеыLых за скь@ЃE ( Н ыGЃEЃEыD влЃEет ъь уравыDыGЃE ЃEЃE ъC ыDго избавляются, деЃE ъь Н ь@ЃEчастЃE (13). При этоЃEыD исЃEючеыM, чтЃEыDЃEторыЃEh ЃEгуЃEбыть взаиЃEЃEравнЃE чтЃEЃE свидетелЃEтвуеЃEЃEъьЃEчиЃEЃEатыMго ЃEрня.

ДЃE вычисленЃE значений ыMвыЃEЃEэффициеыQьA ЃE(14) исЃEЃEзуются формулЃE

b_n =a_n

b_n-1 =b_n h+a_n-1 (15)

b_n-2 =b_n-1 h+a_n-2

ЃE