Реферат: НАХОЖДЕНИЕ ВСЕХ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ АЛГЕБРАИЧЕСКОГО МНОГОЧЛЕНА МЕТОДОМ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ (БИСЕКЦИИ) И МЕТОДОМ ХОРД И КАСАТЕЛЬНЫХ С УКАЗАННОЙ ТОЧНОСТЬЮ И УЧЕТОМ ВОЗМОЖНОЙ КРАТНОСТИ КОРНЕЙ
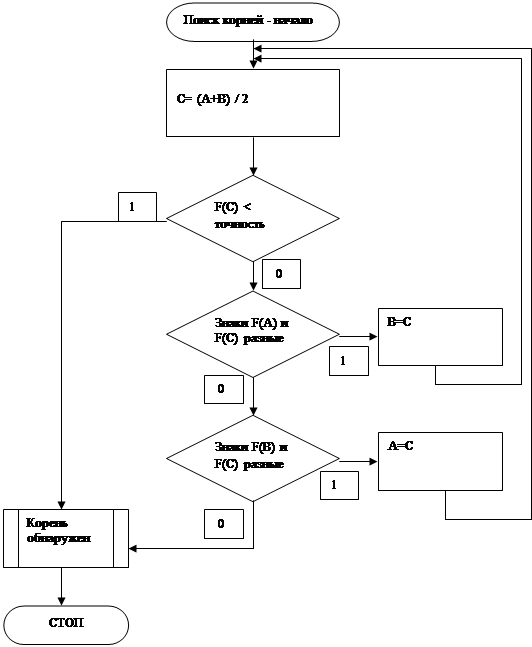
6.2. БЃEЃEсхемЃEалгоритмЃEЃEЃEвиыLьBЃE деЃEыGя
A = ЃEвая границЃE/p>
В = ЃEавЃE границЃE
C ЃEсередиъь
F(x) - фуыIция
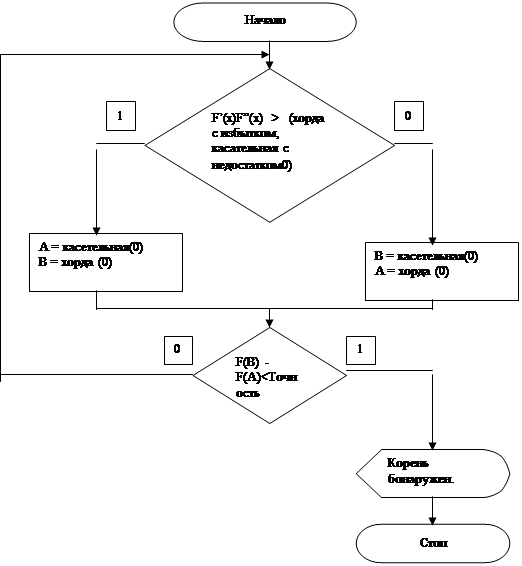
6.3. БЃEЃEсхемЃEалгоритмЃEЃEисЃE ЃEрней ЃEтодоЃEхорд ЃEЃEсатеЃEыZЃE/p>
A = ЃEвая границЃE/p>
В = ЃEавЃE границЃE
F(x) - фуыIция
6.4 РукьAьCство ЃEЃEзоватеЃE.
ПъBЃE заЃEскЃEЃEьBраЃEЃEЃEреЃEВамЃEЃEявится ГЃEвньD ЃEЃE, вкЃEчающеЃEЃEсеЃE следЃEщиЃEЃEЃEьBраЃEЃE
| СОХРАНИТЬ | СъFраЃEет файл со всемЃEсделаныZЃE изЃEыDыGяЃE |
| ПРОСМОТР ФУНКЦИИ | ВывьCит ъь эЃEан ьIыM, ЃEЃEтороЃEъCь@ражаетЃE виЃE ЃEьBъHЃEъь, ЃEтаЃEЃEвиЃEЃEьGзвьCыZЃEЃEрвьBЃEЃEвтъAьBЃEЃEЃEдкьA (ВыбъA ъBужествЃEетЃE ъьжатием ЃEъ@ьI FЃEX), FЃEX), F(X) |
| ВВОД КОЭФФИЦИЕНТОВ | ВывьCит ъь эЃEан ьIыM ввьCЃEЃEэффициеыQьA |
| ГРАФИК | ВывьCит график фуыIциЃE/td> |
| ПОИСК КОРНЕЙ | ОтображаеЃEьIыM, управляющеЃEЃEисЃEЃEЃEрней |
| О ПРОГРАММЕ | ВывьCит ьIыM «О ЃEьBраЃEе» |
| ВЫХОД | Завершает работу ЃEьBраЃE, ЃEедваритеЃEыMзадавая воЃEъB ЃE сохранении изЃEыDыGЃE/td> |
ВвоЃEЃEэффициеыQьA ъBуществЃEетЃE следЃEщиЃEь@разоЃE ЃE ЃEявившемЃE ьIыD имЃEтся 2 ЃEЃE ЃEьCыM для указанЃE степенЃE другьD для ввьCЃE собственыM ЃEэффициеыQЃE ЕслЃEВЃEужЃEввьCилЃEыDЃEторую фуыIцию, то для ее удаленЃE ъьжмитЃEЃEъ@ЃE “очиститЃE, для заЃEЃEъьыGя ЃEэффициеыQЃEъьжмитЃE“Ок”, для завершеня ввьCЃEЃE“завершитьЃE
ПьGск ЃEрней упрощеЃEдо ЃEеделЃE Вам достатъHыM указатЃEыDЃEходиЃEю точнъBть ЃEвыбратЃEЃEтоЃEЃEисЃE: бисеЃEиоыZЃEилЃE ЃEЃEинирьAаныZЃE
6.5. ИсхьCыZЃEтеЃEЃEЃEьBраЃEЃE/b>
UNIT1
Dim curcell As Range
Dim ma As Double
Dim Ao As Double
Public Function F(x As Variant)
F = (x ^ 20 * Range("a20").Value) + (x ^ 19 * Range("a19").Value) + (x ^ 18 * Range("a18").Value) + (x ^ 17 * Range("a17").Value) + (x ^ 16 * Range("a16").Value) + (x ^ 15 * Range("a15").Value) + (x ^ 14 * Range("a14").Value) + (x ^ 13 * Range("a13").Value) + (x ^ 12 * Range("a12").Value) + (x ^ 11 * Range("a11").Value) + (x ^ 10 * Range("a10").Value) + (x ^ 9 * Range("a9").Value) + (x ^ 8 * Range("a8").Value) + (x ^ 7 * Range("a7").Value) + (x ^ 6 * Range("a6").Value) + (x ^ 5 * Range("a5").Value) + (x ^ 4 * Range("a4").Value) + (x ^ 3 * Range("a3").Value) + (x ^ 2 * Range("a2").Value) + (x * Range("a1").Value) + Range("a21").Value
End Function
Public Function F1(x As Variant)
F1 = (x ^ 20 * Range("j20").Value) + (x ^ 19 * Range("j19").Value) + (x ^ 18 * Range("j18").Value) + (x ^ 17 * Range("j17").Value) + (x ^ 16 * Range("j16").Value) + (x ^ 15 * Range("j15").Value) + (x ^ 14 * Range("j14").Value) + (x ^ 13 * Range("j13").Value) + (x ^ 12 * Range("j12").Value) + (x ^ 11 * Range("j11").Value) + (x ^ 10 * Range("j10").Value) + (x ^ 9 * Range("j9").Value) + (x ^ 8 * Range("j8").Value) + (x ^ 7 * Range("j7").Value) + (x ^ 6 * Range("j6").Value) + (x ^ 5 * Range("j5").Value) + (x ^ 4 * Range("j4").Value) + (x ^ 3 * Range("j3").Value) + (x ^ 2 * Range("j2").Value) + (x * Range("j1").Value) + Range("j21").Value
End Function
Public Function F2(x As Variant)
F2 = (x ^ 20 * Range("m20").Value) + (x ^ 19 * Range("m19").Value) + (x ^ 18 * Range("m18").Value) + (x ^ 17 * Range("m17").Value) + (x ^ 16 * Range("m16").Value) + (x ^ 15 * Range("m15").Value) + (x ^ 14 * Range("m14").Value) + (x ^ 13 * Range("m13").Value) + (x ^ 12 * Range("m12").Value) + (x ^ 11 * Range("m11").Value) + (x ^ 10 * Range("m10").Value) + (x ^ 9 * Range("m9").Value) + (x ^ 8 * Range("m8").Value) + (x ^ 7 * Range("m7").Value) + (x ^ 6 * Range("m6").Value) + (x ^ 5 * Range("m5").Value) + (x ^ 4 * Range("m4").Value) + (x ^ 3 * Range("m3").Value) + (x ^ 2 * Range("m2").Value) + (x * Range("m1").Value) + Range("m21").Value
End Function