Реферат: Некоторые темы геометрии

Прямой линией назовем пересечение двух плоскостей в пространстве. Определение можно записать математически как .

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ

Пусть плоскости a и b (рис. 6) за­да­ны уравнениями:

и

,

где ; ,

система из этих уравнений:

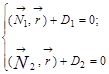Уравнения называются общими уравнениями прямой в

пространстве, записанными в векторной форме.

ТЕМА 6Матрицы и определители.

МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

Матрицей A называется любая прямоугольная таблица, составлен­ная из чисел , которые называют элементами матрицы и обозначается

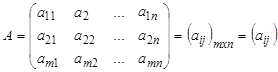Если в выражении (1) , то говорят о квадратной матрице, а если , то о прямоугольной.

Суммой двух матриц и называется матрица C , у которой , и записывают .

Произведением матрицы на число называется такая

матрица C = (c_ij ), у которой (c_ij ) = (ka_ij ).

Если матрица A не нулевая, т.е. существует хотя бы один элемент матрицы A, отличный от нуля, тогда всегда можно указать натуральное число та­кое, что 1) у матрицы A имеется минор го порядка ; 2) всякий минор матрицы A порядка и выше равен нулю, тогда число , обладающее указанными свойствами называется рангом матрицы A и обозначается . Из определения вытекает, что 1) ранг любой прямоугольной матрицы не должен быть больше, чем минимальный размер матрицы. Если матрица квадратная, то ранг не может быть больше, чем размер матрицы. Математически это можно выразить так 2) если все элементы матрицы A равны нулю, т. е. ,то ранг этой матрицы тоже будет равен нулю .

ОПРЕДЕЛИТЕЛИ ИХ СВОЙСТВА

Определителем n-го порядка называется число равное алгебраической сумме , где есть алгебраические дополнения элемента , а - есть соответствующие миноры, т.е. определители (n-1)-го порядка, получающиеся из исходного определителя вычеркиванием первой строки и n-го столбца, на пересечение которых находится элемент .

Количество строк (или столбцов) в определителе называется порядком определителя

СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ.

Решением системы называется совокупность из n чисел (с₁ , с₂ , ..., с_n ), которые, будучи подставленными в систему на место неизвестных x₁ , x₂ , ..., x_n , обращают все уравнения системы в истинные равенства

Систему уравнений, имеющую хотя бы одно решение, называют совместной , систему, не имеющую решений, - несовместной.

Решения и считают различными , если хотя бы одно из чисел не совпадает с соответствующим числом

Если совместная система имеет единственное решение, то она называется определнной ; если совместная система имеет по крайней мере два различных решения, то она называется неопределенной.

Формулы Крамера.

Метод Гаусса.

Пусть А - невырожденная матрица, то есть det A 0, и, следовательно, она имеет обратную матрицу А^-1 . Умножив обе части на А^-1 слева, получаем:

А^-1 (А Х) = А^-1 В (А^-1 А)Х = А^-1 В Е Х = А^-1 В, то есть Х = А^-1 В и есть искомое решение системы (14). Действительно, подставив (16) в (14), получим А (А^-1 В) = (А^-1 А)В = Е В = В.