Реферат: Нелинейные многоволновые взаимодействия в упругих системах
аналитическое решение которой, удовлетворяющее соответствующим краевым и начальным условиям, представляется суперпозицией нормальных волн
![]() ,
,
где ![]() - постоянные комплексные амплитуды;
- постоянные комплексные амплитуды; ![]() - число нормальных волн
- число нормальных волн ![]() -го типа. Возникает вопрос - есть ли существенная разница между этими двумя системами, иначе говоря, - насколько существенно присутствие малой нелинейности. В соответствии с теорией нормальных форм (см. например [4]), решение уравнений (4) ищется в форме почти тождественного преобразования переменных, т.е.
-го типа. Возникает вопрос - есть ли существенная разница между этими двумя системами, иначе говоря, - насколько существенно присутствие малой нелинейности. В соответствии с теорией нормальных форм (см. например [4]), решение уравнений (4) ищется в форме почти тождественного преобразования переменных, т.е.
(6) ![]()
где ![]() - неизвестная
- неизвестная ![]() -мерная векторная функция, компоненты которой формально представимы рядом по
-мерная векторная функция, компоненты которой формально представимы рядом по ![]() , т.е. почти билинейная форма:
, т.е. почти билинейная форма:
(7) ![]() ,
,
Например
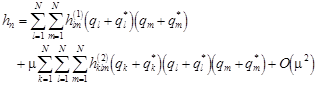
где ![]() и
и ![]() - неизвестные коэффициенты, подлежащие определению. При подстановке (6) в (4), получаются следующие дифференциальные уравнения с частными производными для нахождения
- неизвестные коэффициенты, подлежащие определению. При подстановке (6) в (4), получаются следующие дифференциальные уравнения с частными производными для нахождения ![]() :
:
![]() .
.
Очевидно, что собственные числа оператора ![]() , действующего на полиномиальные компоненты функции
, действующего на полиномиальные компоненты функции ![]() , т.е.
, т.е. ![]() , представляют собой линейные целочисленные комбинации собственных чисел оператора
, представляют собой линейные целочисленные комбинации собственных чисел оператора ![]() при различных значениях векторов
при различных значениях векторов ![]() .
.
В первом приближении получаются линейные уравнения для нахождения нормализующего преобразования:
![]() .
.
Всякой полиномиальной компоненте ![]() соответствует собственное число
соответствует собственное число ![]() , т.е.
, т.е. ![]() , где
, где
![]() или
или
![]() ,
,
в то время как ![]() в наинизшем приближении разложения по
в наинизшем приближении разложения по ![]() .
.
Аналогично, во втором приближении разложения решения по ![]() :
:
![]()
собственные значения оператора ![]() можно выразить в следующем виде:
можно выразить в следующем виде: ![]() , где
, где ![]() . Продолжая и далее подобные итерационные процедуры, можно построить искомое преобразование (7).
. Продолжая и далее подобные итерационные процедуры, можно построить искомое преобразование (7).
Таким образом, если хотя бы одно собственное значение оператора ![]() стремится к нулю,
стремится к нулю, ![]() , то соответствующие коэффициенты ряда (7) стремятся к бесконечности, т.е. говорят, что в системе наступает резонанс порядка
, то соответствующие коэффициенты ряда (7) стремятся к бесконечности, т.е. говорят, что в системе наступает резонанс порядка ![]() . В противном случае, если собственные значения оператора
. В противном случае, если собственные значения оператора ![]() не равны нулю, то системы (4) и (5) называются формально эквивалентными , поскольку ряд (7) все же может быть расходящимся. Если же
не равны нулю, то системы (4) и (5) называются формально эквивалентными , поскольку ряд (7) все же может быть расходящимся. Если же ![]() оказывается ограниченной аналитической функцией, то системы (4) и (5) считаются аналитически эквивалентными .
оказывается ограниченной аналитической функцией, то системы (4) и (5) считаются аналитически эквивалентными .
В теории нормальных форм существует основная теорема Пуанкаре, накладывающая одновременно весьма сильные условия на спектральные параметры системы и на коэффициенты нормализующего преобразования, для того чтобы две подходящие различные системы обыкновенных дифференциальных уравнений оказались аналитически эквивалентными. Во множестве задач о колебаниях нелинейных механических систем условия теоремы Пуанкаре, как правило, не выполняются. Например, основные типы резонансов второго порядка ассоциируются с трехволновыми резонансными процессами, когда ![]() и
и ![]() ; процессом генерации второй гармоники, когда
; процессом генерации второй гармоники, когда ![]() и
и ![]() .
.
Наиболее важные случаи резонансов третьего порядка следующие: четырехволновые резонансные процессы, при выполнении условий синхронизма: ![]() ;
; ![]() (взаимодействие двух пар волн), или при иных условиях синхронизма
(взаимодействие двух пар волн), или при иных условиях синхронизма ![]() и
и ![]() (распад высокочастотной волны на тройку низкочастотных волн); вырожденные трехволновые резонансные процессы, при
(распад высокочастотной волны на тройку низкочастотных волн); вырожденные трехволновые резонансные процессы, при ![]() и
и ![]() ; генерация 3-ей гармоники, при
; генерация 3-ей гармоники, при ![]() и
и ![]() .
.
Во всех приведенных примерах резонансов второго и третьего порядков в общем случае наблюдается ярко выраженная амплитудная модуляция , глубина которой растет, когда фазовая расстройка стремится к нулю. Волны, фазы которых удовлетворяют условиям фазового синхронизма, формируют так называемые резонансные ансамбли .
Наконец, во втором нелинейном приближении всегда присутствуют так называемые нерезонансные взаимодействия , когда условия фазового синхронизма вырождаются в следующие “тривиальные” случаи: кросс-взаимодействия пары волн, при ![]() и
и ![]() ; самовоздействия волны,
; самовоздействия волны, ![]() и
и ![]() .
.
Нерезонансные взаимодействия в основном характеризуются только лишь фазовой модуляцией волн.
Основное предложение настоящего пункта можно сформулировать следующим образом. Если в системе (4) нет резонансов, начиная с порядка ![]() и до порядка
и до порядка ![]()
![]() включительно, то следует ожидать, что нелинейность приведет лишь только к малым поправкам к решениям соответствующей линеаризованной системы. Эти поправки будут того же порядка,
включительно, то следует ожидать, что нелинейность приведет лишь только к малым поправкам к решениям соответствующей линеаризованной системы. Эти поправки будут того же порядка, ![]() , что и мера нелинейности, и вплоть до времен
, что и мера нелинейности, и вплоть до времен ![]() .
.
Для получения формально пригодного преобразования (7) в резонансном случае, следует пересмотреть структуру системы сравнения (5) в сторону модификации ее правой части:
(8) ![]() ;
; ![]() ,
,