Реферат: Нелинейные многоволновые взаимодействия в упругих системах

Теория нормальных форм достаточно просто обобщается на случай так называемых существенно нелинейных систем, поскольку малый параметр может быть опущен в выражениях (4) - (8) без всякого ущерба для конечного результата, при этом и оператор может также зависеть от пространственной переменной .

Формально, собственные значения оператора могут быть произвольными комплексными числами. Это означает то, что резонансы порядка могут быть определены и проклассифицированы даже и для неколебательных процессов, например применительно к эволюционным уравнениям.

Резонанс в многоволновых системах

Явление резонанса играет ключевую роль в динамике большинства физических систем. Интуитивно, резонанс ассоциируется с одним частным случаем силового возбуждения линейных колебательных систем. Такое возбуждение сопровождается с более или менее скорым ростом амплитуды колебаний при достаточной близости одной из собственных частот колебаний системы к частоте внешнего периодического возмущения. В свою очередь, в случае так называемого параметрического резонанса возникают некоторые рациональные соотношения между собственными частотами системы и частотой параметрического возмущения. Таким образом, резонанс можно проще всего классифицировать, согласно выше приведенному эскизу, по его порядку, начиная с первого, , если включить в рассмотрение и линейные и нелинейные динамические системы. Поэтому, в общем случае, понятие резонанса в колебательных системах может быть связано с физическим явлением, которое характеризуется накоплением энергии одним или несколькими колебательными объектами за счет энергии другой группы колебательных объектов, когда все колебательные процессы объединены некоторым пространственно-временным сродством. Так называемые нерезонансные процессы, такие как кросс-взаимодействия и самовоздействие, также могут быть включены в подобное определение, но со специальной оговоркой, касающейся их специфических динамических свойств.

Для широкого класса механических систем со стационарными краевыми условиями математическое определение резонанса следует из рассмотрения следующих усредненных функций

(9) , при ,

где - комплексные константы соответствующие решениям линеаризованных эволюционных уравнений (5); - пространственный объем, занимаемый системой. Если функция претерпевает скачек при заданных значениях и , то систему следует отнести к резонансной[5] . Последнее подтверждается основными результатами теории нормальных форм. Резонанс имеет место при условии выполнения условий фазового синхронизма

и .

Здесь - число резонансно взаимодействующих квазирармоник; - некоторые целые числа ; и - параметры малой расстройки.

Пример 1. Рассматриваются линейные поперечные колебания тонкой балки, подверженной действию малой внешней периодической силы и параметрического возбуждения, согласно уравнению

,

где , , , , , и - некоторые подходящие константы, . Это уравнение переписывается в стандартной форме

,

где , , . При , решение уравнения таково, где собственные частоты удовлетворяют дисперсионному соотношению . Если , тогда малые амплитудные вариации удовлетворяют следующему уравнению

где , - групповая скорость амплитудной огибающей. Усреднение правой части этого уравнения, в соответствии с (9), дает

, при ;

, при и ;

во всяком другом случае.

Отметим, что резонансные свойства системы с нестационарными краевыми условиями не всегда могут быть обнаружены с помощью функции .

Пример 2. Рассматриваются уравнения, описывающие колебания балки по модели Бернулли-Эйлера:

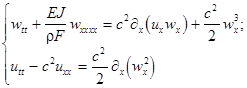
с граничными условиями ; ; . После приведения уравнений к стандартной форме и использовании формулы (9), определяется скачек функции при условиях

и .

В то же время, резонанс первого порядка, испытываемый продольной волной на частоте , автоматически уже не определяется.

Литература

1. Kaup P. J., Reiman A. and Bers A. Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys., (1979) 51 (2), 275-309.

2. Ковригин Д.А., Потапов А.И. Нелинейная волновая динамика одномерных упругих систем. Изв. вузов. ПНД , (1996) 4 (2), 72-102.

3. Маслов В.П. Операторные методы . М.: Наука, 1973, с.544.

4. Jezequel L., Lamarque C. - H. Analysis of nonlinear dynamical systems by the normal form theory, J. of Sound and Vibrations , (1991) 149 (3), 429-459.