Реферат: Нелинейные САУ

и уравнения имели только одно общее решение: х₁ = х₂ =0. В плоскости х_1, х₂ этм условия в случае линейной системы определяют две прямые линии, пересекающиеся в начале координат (рис.1, а). Если же функции f₁ (х₁ , x₂ ) и f₂ (х₁ , х₂ ) нелинейны, то кривые, соответствующие уравнениям, могут пересекаться и вне начала координат. Система имеет в этом случае, кроме ре­шения х₁ , =х₂ = 0, и другие решения. В этом случае, кроме регулируемого режима, соответствующего началу координат, в системе возможны и иные положения равновесия (рис.1, б), и характер движения в системе зависит от величины отклонения от начала координат, вызванного возмущением.

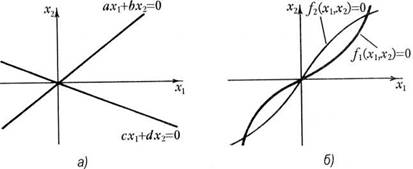
Рис.1 Графики, соответствующие уравнениям для линейной (а) и нелинейной (б) систем

В рассматриваемом нелинейном случае особые точки могут быть лишь тех же типов, что и в линейной системе (фокусы, узлы и седла). Чтобы в нелинейном случае определить тип особой точки, надо составить соответствующее этой особой точке уравнение линейного приближения, разложив в окрестности этой точки в ряды правые части уравнений и сохранив затем в этих рядах только линейные члены. Эта операция эквивалентна «локальной» линеаризации системы вблизи особой точки.

На рис.2, а в качестве примера показан фазовый портрет системы для случая, когда кривые f₁ (х₁ , x₂ ) = 0 и f₂ (х₁ , х₂ ) = 0 пересекаются в двух точках. Кроме начала координат, где находится особая точка — аттрактор — устойчивый фокус, они пересекаются ещё в одной точке — неустойчивом узле, где располагается седло. Жирной линией показана траектория, проходящая через седло и выделяющая область притяжения устойчивого равновесного режима, то есть аттрактора типа «устойчивый фокус», расположенного в начале координат (эта область заштрихована на рисунке).

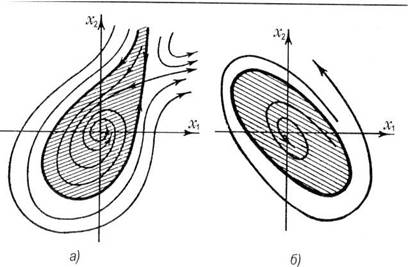
Рис.2. Фазовые портреты нелинейных систем: а — с устойчивым фокусом и седлом, б — с устойчивым фокусом и предельным циклом. В обоих случаях имеются заштрихованные области устойчивости

До тех пор, пока изображающая точка на фазовой плоскости рис. 2, а находится внутри заштрихованной области, с течением времени фазовые траектории системы будут стремиться к началу координат, и по отношению к таким начальным состояниям система является устойчивой. Если же в результате возмущения изображающая точка окажется вне заштрихованной области, то исходящая из этой точки фазовая траектория уходит в бесконечность, и по отношению к такому возмущению система неустойчива. Заштрихованную область притяжения особой точки, расположенной в начале координат, поэтому можно назвать областью устойчивости системы. Фазовый портрет, показанный на рис. 2, а, так же, как и фазовый портрет линейной системы, не содержит замкнутых фазовых траекторий. Между тем в нелинейных системах, как в том случае, когда имеется одна особая точка, так и в случае нескольких особых точек, могут содержаться замкнутые траектории.

На рис.2, б показан пример системы, имеющей только одну особую точку в начале координат (устойчивый фокус) и одну замкнутую траекторию, охватывающую начало координат. Фазовые траектории не могут пересекаться где-либо вне особой точки, и поэтому замкнутая траектория (ее называют предельным циклом) отделяет область притяжения особой точки — заштрихованную область устойчивости системы от «внешней» части фазовой плоскости, где система неустойчива. Внутри предельного цикла фазовые траектории «сматываются» с него и «наматываются» на начало координат. Снаружи фазовые траектории «разматываются» с предельного цикла, и по любой фазовой траектории изображающая точка уходит в бесконечность. Сам предельный цикл соответствует незатухающим колебаниям, но в данном случае они неустойчивы, поэтому такой предельный цикл называется неустойчивым предельным циклом. Достаточно сколь угодно малого возмущения, чтобы изображающая точка, сойдя с предельного цикла, более уже не возвращалась на него, а перемещалась бы по соответствующей траектории к началу координат или в бесконечность. Незатухающие колебания в такой системе реально не наблюдаются, а роль предельного цикла состоит лишь в ограничении области действия аттрактора.

Другой пример системы, имеющей одну особую точку («неустойчивый фокус») и один охватывающий ее предельный цикл, показан на рис.3, а.

Здесь положение равновесия неустойчиво, но «область отталкивания» или неустойчивости системы ограничена предельным циклом (эта область заштрихована на рис.3, а). При начальном положении изображающей точки внутри заштрихованной области система будет двигаться по траектории, соответствующей колебаниям с нарастающей амплитудой, и постепенно в системе установятся незатухающие колебания, соответствующие предельному циклу. Наоборот, при начальном положении вне заштрихованной области, колебания затухают до тех пор, пока точка не попадёт на предель­ный цикл, и установятся колебания, соответствующие предельному циклу. Он в этом случае не только разделяет две области фазового портрета, но и определяет устойчивые незатухающие колебания в системе {устойчивый предельный цикл). В данном случае предельный цикл является аттрактором.

На рис.3, б показан фазовый портрет системы, содержащий два предельных цикла, охватывающих единственную особую точку — устойчивый фокус. Эта система имеет два аттрактора.

Область притяжения первого аттрактора — фокуса в начале координат, соответствующего регулируемому равновесию, ограничена внутренним неустойчивым предельным циклом.

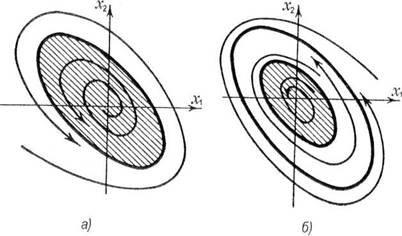
Рис. 3 Фазовые портреты нелинейных систем с предельными циклами: а — в системе один аттрактор — устойчивый предельный цикл, его область притяжения — вся фазовая плоскость, б — система с двумя предельными циклами (устойчивым и неустойчивым) и одним устойчивым фокусом

Если возмущения не выводят систему за пределы области, охватываемой внутренним предельным циклом, положение равновесия восстанавливается и система сохраняет устойчивость. Если же система окажется вне внутреннего предельного цикла, она попадает в область притяжения второго аттрактора — внешнего устойчивого предельного цикла, и в системе с течением времени устанавливаются незатухающие колебания, соответствующие внешнему циклу.

На рис.4, а показан аналогичный фазовый портрет для случая, когда положение регулируемого равновесия неустойчиво, и в начале координат располагается неустойчивый фокус. Если начальное состояние этой системы лежит в любой точке фазовой плоскости, лежащей внутри внешнего предельного цикла, то в системе устанавливаются незатухающие колебания, соответствующие единственному аттрактору — внутреннему предельному циклу. Если же начальное состояние окажется вне внешнего предельного цикла, то в системе возникают колебания, амплитуда которых неограниченно растет.

Система может иметь предельные циклы и тогда, когда фазовый портрет содержит более одной особой точки. Пример такого рода показан на рис.4, б. Здесь регулируемое равновесие неустойчиво(в начале координат — неустойчивый фокус), предельному циклу соответствуют устойчивые незатухающие колебания, которые устанавливаются с течением времени, если начальная точка лежит внутри области, выделенной фазовой траекторией, проходящей через вторую особую точку — седло. Эта траектория выделена на рис.4., б жирной линией.

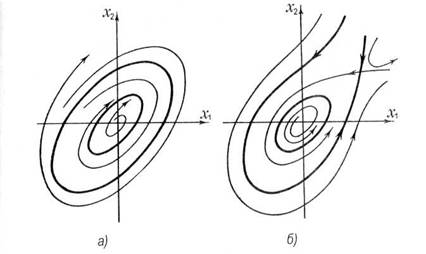
Рис.4. Фазовые портреты нелинейных систем, не имеющих устойчивых особых точек: а — система с двумя предельными циклами, из которых только внутренний устойчив, б — система с устойчивым предельным циклом и седлом

Если фазовый портрет системы содержит более одной особой точки или если он содержит замкнутые траектории (предельные циклы), то область устойчивости не может охватывать всей фазовой плоскости подобно тому, как это имеет место в линейной системе. В этом случае область устойчивости всегда ограничена предельным циклом или фазовой траекторией, проходящей через особую точку.

Разумеется, фазовый портрет нелинейной системы может и не содержать дополнительных особых точек или замкнутых траекторий. В этом случае область влияния начала координат фазового пространства может охватывать всю фазовую плоскость и, так же, как в линейной системе, устойчивость не зависит от величины начального положения изображающей точки и величины возмущений.

До сих пор рассматривалась система, для описания которой достаточно двух уравнений первого порядка

В большинстве случаев при решении практических задач теории автоматического регулирования приходится иметь дело с уравнениями более высоких порядков.

Если порядок уравнения системы п больше, чем второй, то вместо двумерного фазового пространства — плоскости рассматривают n -мерное пространство, то есть такое пространство, в котором для задания точки надо задать п чисел — координат.

Если система дифференциальных уравнений имеет периодическое решение, то этому решению в фазовом пространстве соответствует замкнутая кривая. На плоскости замкнутые кривые являлись границами областей. В пространстве же ограничивать определенные области могут только поверхности, а не кривые. Поэтому замкнутая траектория по-прежнему соответствует периодическому решению рассматриваемой системы дифференциальных уравнений, но не служит границей области.

Существуют два принципиальных различия между фазовой плоскостью и фазовым пространством.

1. На фазовой плоскости предельный цикл является не только образом колебательного движения, но и границей области устойчивости для другого предельного цикла или особой точки.