Реферат: Непрерывная ректификация

Р = p_A+p_B=P_Ax_A+P_B(1-x_B)=P_B+(P_A-P_B)x_A (1.5.)

тогда

x_A=(P-P_B)/(P_A-P_B) (1.6.)

По уравнению (1.6.)) по известным Р_А и Р_B при заданной температуре t₁ , t₂ и т.д. находят х_A , х_B и т.д., а затем по уравнению (1.4.) -соответствующие значения у*_A1 , у*_А2 и т.д. и по найденным точкам строят линии кипения жидкости (кривая t_AA₂A₁t_B) и конденсации паров (кривая t_AB₂B_lt_B). Отметим, что уравнение (1.6.) устанавливает связь между концентрациями (по жидкости) и заданными давлениями (общим Р и насыщенных паров Р_А и Р_B). Отрезки А₁В₁ , А₂ В₂ и т. д., соединяющие точки равновес­ных составов жидкой и паровой фаз, являются изотермами.

Отметим, что точки, лежащие на кривой t_AA₂A₁t_B,, отвечают жидкой фазе, находящейся при температуре кипения. Очевидно, что любая точка, лежащая ниже этой кривой, характеризует систему, состоящую только из жидкой фазы. Аналогично, любая точка лежащая выше кривой t_A B₂ В₁ t_B , характеризует систему, темпера тура которой выше температуры начала конденсации пара, т. е пары в этой точке являются перегретыми, и система состоит только из паровой фазы. Точки, находящиеся между кривыми кипения и конденсации (например, точка С на рис. 1.2.), характеризуют системы, температуры которых выше температуры кипения жидко­сти данного состава и ниже температуры конденсации паров этого же состава. Таким образом, эти точки отвечают равновесным парожидкостным системам.

Основные положения фазового равновесия были рассмотрены в гл. 2 (правило фаз Гиббса, законы Генри и Рауля и др.). Там же для идеальных бинарных систем получено уравнение (1.7.), которое описывает линию равновесия:

у*_А = ах_А/[1+х_А(а-1)], (1.7.)

где а = Р_А/Р_В - относительная летучесть компонента А (иногда а называют коэффи­циентом разделения).

Очевидно, что для смеси, состоящей из n компонентов, например, А, В, С, D, на основе законов Рауля и Дальтона имеем

y_A = (Р_A/Р)х_A; y_B = (Р_B/Р)х_B; y_C = (Р_C/Р)х_C; y_D = (Р_D/Р)х_D. (1.8.)

Поскольку

P=P_Ax_A+ P_Bx_B+ P_Cx_C+ P_Dx_D+ …= (1.9.)

то для любого j-го компонента

y_j = P_jX_j/. (1.10.)

Разделив числитель и знаменатель правой части уравнения (1.10) на величину Р_А, получим

y_j = а _jX_j/, (1.11.)

где а _A = Р_А/Р_В ; а _в = Р_В/Р_А ; а _C = Р_С/Р_А и т. д.

Например, зависимость давления насыщенного пара от темпера­туры хорошо описывается эмпирическим уравнением Антуана

lnР_А = А - В/(Т+ C), (1.12.)

где А - постоянная, не зависящая от температуры; В и С -константы, определяемые по справочникам; T- абсолютная температура.

Уравнение (5.12) описывает температурную зависимость давле­ний паров в интервале температур до нескольких десятков градусов и при давлениях, не слишком близких к критическим.

Взаимное положение кривых на фазовых диаграммах t — х — у и у — х как для идеальных, так и для реальных систем могут быть определены с помощью законов Коновалова. Законы Коновалова устанавливают связи между изменениями состава, давления или температуры в двухфазных системах, они лежат в основе теории перегонки и ректификации бинарных смесей.

Первый - закон Коновалова формулируется так: пар обогащается тем компонентом, при добавлении которого к жидкости повышает­ся давление пара над ней или снижается ее температура кипения, или пар всегда более обогащен НК, чем соответствующая ему равновесная жидкая фаза.

Первый закон Коновалова дополняется первым правилом Врев­ского, отражающим влияние температуры на равновесные составы фаз: при повышении температуры бинарной смеси в парах возрас­тает относительное содержание того компонента, парциальная молярная теплота испарения которого больше.

Это можно проиллюстрировать с помощью фазовой диаграммы (рис. 1.2.). Для идеальной смеси очевидно, что при одной и той же температуре t содержание НК в парах у*_A1 (точка B₁ больше его содержания х_а в равновесной с парами жидкости (точка А₁). При добавлении к смеси НК ее температура кипения снижается, но содержание НК в паре остается выше, чем в жидкости.

Реальные жидкие смеси могут значительно отклоняться от закона Рауля. Если зависимость полного давления (или сумма парциальных давлений) паров от состава жидкой смеси проходит выше линий, характеризующих те же зависимости для идеальных смесей (рис. 1.3.), то такое отклонение называют положительным, если ниже - отрицательным отклонением от закона Рауля. Эти отклонения определяются изменением активности молекул в раст­воре, диссоциацией, гидратацией и др. Степень отклонения реаль­ной системы от закона Рауля выражают величиной коэффициента активности :

p_A = P_Ax_A . (1.13.)

Для смесей с положительным отклонением от закона Рауля
> 1, для смесей с отрицательным отклонением — < 1. Отметим, что определение значений у часто затруднительно, поэтому диа­граммы P — х обычно строят по экспериментальным (справочным) данным.
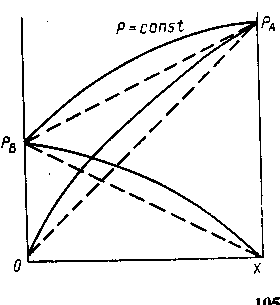