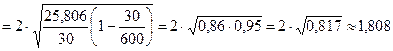Реферат: Нормирование оборотных фондов

= = =млн.руб.

Коэффициент вариации рассчитывается на основе выше найденных значений по формуле:

V=%

V =

4) Вычислим среднюю арифметическую (простую) по исходным данным, т.е. для несгруппированного ряда:

млн. руб.,

где х – значение признака, n – число единиц признака.

Если сравнить два аналогичных показателя средней арифметической, то можно заметить небольшое расхождение (разница составляет 0,333 млн.руб.). Это объясняется тем, что при расчете средней арифметической по ряду распределения возникает ошибка, связанная с тем, что мы используем значение середины интервала, а не исходные данные.

По величине коэффициента вариации можно оценить интенсивность колебаний вариантов относительно их средней величины.В нашем случае колеблемость незначительна для обоих признаков, т.к. V _s = 24,6% < 40%. Кроме того, можно судить об однородности состава совокупности. Чем больше величина коэффициента, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. В нашей задаче совокупность однородная.

Гистограмма имеет одновершинную форму: с возрастанием признака частоты вначале также возрастают, а затем, достигнув в середине ряда своей максимальной величины, - уменьшаются по мере дальнейшего роста значений признака. Поэтому есть основания предполагать, что выборка является однородной по данному признаку. Можно сделать вывод, что распределение единиц по изучаемому признаку будет близко к нормальному (= Mo = Me ) .

ЗАДАНИЕ 2

Таблица 5

Группировка данных в порядке возрастания (по х)

№ предприятия	Среднегодовая стоимость материальных оборотных фондов, млн.руб. (х)	Выпуск продукции, млн.руб. (у)	У2
28	10	24	576
30	11	19	361
12	12	21	441
11	13	35	1225
29	14	36	1296
7	15	30	900
14	17	41	1681
15	17	30	900
26	18	35	1225
3	18,3	34	1156
6	19	38	1444
2	19,8	35	1225
22	19,9	45	2025
10	20,7	38	1444
16	21,3	47	2209
17	21,7	42	1764
9	22,8	46	2116
23	22,9	43	1849
13	23,5	27	729
21	23,7	48	2304
27	23,8	40	1600
1	24,7	39	1521
5	24,9	50	2500
18	26	34	1156
8	27	51	2601
19	27	57	3249
4	28	61	3721
24	29	48	2304
25	29	60	3600
20	30	46	2116
Σ	630	1200	51238

1) Построим рабочую таблицу – проведем группировку по факторному признаку (х): число групп – 4, величина интервала была рассчитана ранее и равна 5. Полученные результаты представлены в таблице 6.

Таблица 6.

Группировка предприятий по факторному признаку (х)

№ предприятия	Среднегодовая стоимость материальных оборотных фондов (х)	Выпуск продукции (у)
28	10	24
30	11	19
12	12	21
11	13	35
29	14	36
Итого:5	60	135
7	15	30
14	17	41
15	17	30
26	18	35
3	18,3	34
6	19	38
2	19,8	35
22	19,9	45
Итого:8	144	288
10	20,7	38
16	21,3	47
17	21,7	42
9	22,8	46
23	22,9	43
13	23,5	27
21	23,7	48
27	23,8	40
1	24,7	39
5	24,9	50
Итого:10	230	420
18	26	34
8	27	51
19	27	57
4	28	61
24	29	48
25	29	60
20	30	46
Итого:7	30	46

Вычислим средний выпуск продукции:

=

=

Установим наличие и характер связи между признаками методом аналитической группировки. Построим аналитическую таблицу 7.

Таблица 7

Аналитическая таблица

Группы предприятий по факторному признаку (х)	Число предприятий, fi	Среднегодовая стоимость материальных оборотных фондов, млн.руб. (х)		Выпуск продукции, млн.руб. (у)		(- )2	(- )2 ni
		Всего, млн.руб.	В среднем на одно предприятие,	Всего, млн.руб.	В среднем на одно предприятие,
[10;15)	5	60	12	135	27	169	845
[15;20)	8	144	18	288	36	16	128
[20;25)	10	230	23	420	42	4	40
[25;30]	7	196	28	357	51	121	847
Итого	30	630	1200	1860

Анализ таблицы 7 показывает, что с ростом среднегодовая стоимость материальных оборотных фондов от группы к группе возрастает и выпуск продукции.

Построим корреляционную таблицу 8, предварительно проведя группировку по результативному признаку (у): число групп – 4, величину интервала определим аналогично факторному признаку по формуле: = (млн.руб.)

Таблица 8

Корреляционная таблица

Среднегодовая стоимость материальных оборотных фондов	Объем реализованной продукции, млн. руб.
	19-29,5	29,5-40	40-50,5	50,5-61	Итого:
10.-15	3	2	5
15-20	6	2	8
20-25	1	2	7	10
25-30	1	2	4	7
Итого	4	11	11	4	30

Так как ненулевые значения в таблице расположены в основном по главной диагонали, можно сделать вывод о прямой и тесной зависимости между переменными.

2) Измерим тесноту корреляционной связи между признаками Х и У с использованием коэффициента детерминации (η² ) и эмпирического корреляционного отношения.

Коэффициент детерминации показывает долю вариации результативного признака (У) под влиянием факторного (Х):

η² = ,

где δ² – межгрупповая дисперсия, σ² – общая дисперсия.

- ²

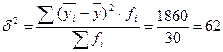
η² = =

Коэффициент детерминации говорит, что среднегодовая стоимость материальных оборотных фондов на 57% определяет вариацию выпуска продукции.

Эмпирическое корреляционное отношение:

по своей величине достаточно близко к 1, что говорит о наличии достаточно тесной связи между признаками.

Задание 3.

1. Средняя ошибка выборки в случае бесповторного отбора для средней вычисляется по формул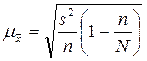е: , где

– средняя ошибка выборочной средней;

– дисперсия выборочной совокупности;

− доля выборки. Так как по условию выборка 20%-ная, то =0,05

Тогда предельная ошибка для средней будет равна:

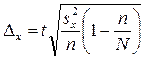
Так как по условию ошибку надо гарантировать с вероятностью 0,954, то коэффициент доверия t =2. Из расчетов задачи 1 дисперсия равна 5,08² =25,806