Реферат: О некоторых применениях алгебры матриц
не имеет решений в натуральных числах ![]() .
.
Предложение 2 . Уравнение
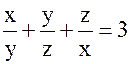
разрешимо в натуральных числах ![]() .
.
Доказательство : удовлетворяют нашему уравнению. Если не все три числа 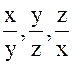 между собой равны, то как мы видели в ходе доказательства Предложения (1), выполняется неравенство
между собой равны, то как мы видели в ходе доказательства Предложения (1), выполняется неравенство
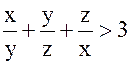
- противоречие. Таким образом, должно быть 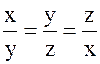 , и из нашего уравнения следует, что каждое из этих чисел равно 1, так что
, и из нашего уравнения следует, что каждое из этих чисел равно 1, так что ![]() .
.
Поэтому получаем
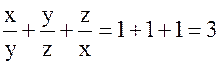 .
.
Итак, мы доказали, что заданное уравнение имеет бесконечно много решений в натуральных числах ![]() .
.
Предложение 3 . Произведение двух чисел, каждое из которых является суммой двух квадратов, представимо в виде суммы двух квадратов.
Доказательство : Рассмотрим следующее произведение двух циклических матриц (второго порядка)
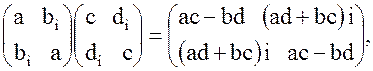
где ![]() - мнимая единица. Переходя к определителям, получим равенство
- мнимая единица. Переходя к определителям, получим равенство
![]() . (5)
. (5)
Предложение 4 . Если число представляемое в виде суммы двух квадратов, делится на простое число, являющееся суммой двух квадратов, то частное также является суммой двух квадратов.
Доказательство : Пусть число ![]() делится на простое число
делится на простое число ![]() вида
вида ![]() :
:
![]() .
.
Требуется доказать, что частное ![]() имеет вид
имеет вид ![]() .
.
Предположим, что задача уже решена, т.е.
![]() , (6)
, (6)
и с помощью анализа попробуем найти искомые числа ![]() и
и ![]() . Гипотетическое равенство (6) подсказывает целесообразность рассмотрения матричных равенств.
. Гипотетическое равенство (6) подсказывает целесообразность рассмотрения матричных равенств.
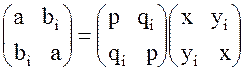
и
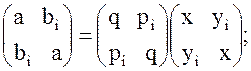
перемножив правые части этих равенств, получим:
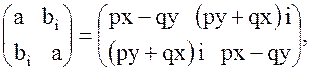
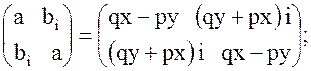
отсюда имеем:
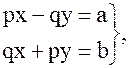
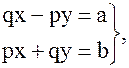
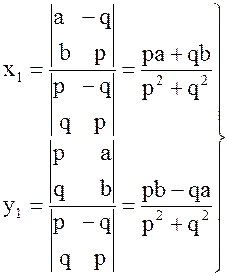 (7)
(7)
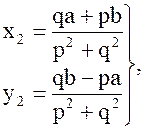 (8)
(8)
![]() . (9)
. (9)
Так как ![]() - простое число и
- простое число и ![]() делит
делит ![]() , то равенство (9) показывает, что
, то равенство (9) показывает, что ![]() или
или ![]() делится на
делится на ![]() .
.