Реферат: Об алгоритмах самоорганизации в задаче синтеза информационных технологий обработки сигналов
Отклик
(выход)
На самом же деле это не так! Дело в том, что момент начала кристаллизации, определяется множеством внешних факторов (начальной температурой расплава, условиями теплообмена и т.п.). А это значит, что для различных наблюдений в выборке, температуре ликвидуса TL будут соответствовать различные номера дискретных значений 
. Поэтому совершенно очевидно, что без привлечения дополнительной информации при сколь угодно большом объеме W выборки невозможно восстановить истинную зависимость (4) в классе структур (5), поскольку для различных наблюдений аргумент истинной зависимости (4) – температура TL – будет соответствовать различным аргументам моделей (5).
К тому же при больших значениях 
возникают непреодолимые вычислительные проблемы в использовании известных алгоритмов МГУА, но это уже другие проблемы.
Отсюда следует, что важным этапом синтеза ИТ обработки сигналов, предшествующим структурно-параметрической идентификации, является переход от пространства наблюдений 
к пространству потенциально полезных признаков 
меньшей размерности (
), а затем уже этап использования этих признаков в качестве аргументов моделей косвенного контроля и диагностики, селектируемых тем или иным алгоритмом самоорганизации на основе обучающей и контрольной выборок.
Именно такой взгляд на роль алгоритмов МГУА при синтезе прикладных ИТ обработки сигналов в условиях ограниченной априорной информации представляется автору наиболее реалистичным. Структура инструментальной системы “СИДИГРАФ”, реализующая такой подход, обсуждалась в работах [5,12].
Практические результаты. Как уже отмечалось, рассмотренный в предыдущем разделе пример оценки только одного содержания углерода является упрощенной схемой задачи, которая была положена в основу синтеза ИТ “ТЕРМОГРАФ”. Оказалось, что используя всего лишь информацию о дискретных значениях температуры 
в процессе охлаждения пробы удается оценить с приемлемой точностью целый ряд других химических элементов расплава (содержание кремния 
, хрома 
, фосфора 
, марганца 
, и др.), а также прогнозировать механические свойства металла, в частности прочность на растяжение 
и твердость 
.
Переход от пространства наблюдений размерности 
к экономному пространству признаков осуществлялся на основе специальных вычислительных процедур, позволяющих автоматически выделить на термограмме 
и ее первой производной 
информативные фрагменты (см. рис. 7). Границы этих фрагментов (точки) соответствуют характерным тепловым эффектам фазовых превращений металла, а именно
А - максимальному тепловому эффекту дендритной кристаллизации;
B - максимальной скорости охлаждения после периода дендритной кристаллизации;
C - температуре начала кристаллизации эвтектики;
D - температуре метастабильного превращения расплава;
E - максимальному тепловому эффекту процесса кристаллизации эвтектики;
F - температуре солидуса расплава;
G – максимальному изменению скорости охлаждения в период кристаллизации эвтектики;
H - температуре окончания кристаллизации эвтектики;
J - моменту времени, при котором температура расплава становится равной T = 1050 град С.
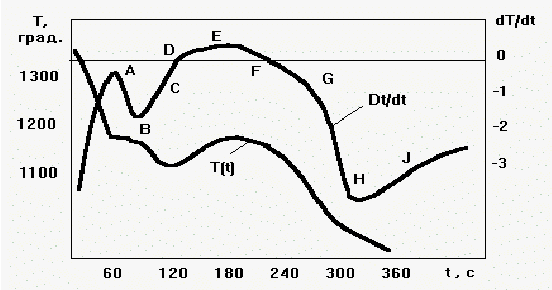
Рис.7. Термограмма и ее первая производная
Для каждой из указанных девяти точек определялась тройка величин 
, (
), представляющих собой момент времени, при которой она появилась, а также значение температуры и оценка ее первой производной в этот момент времени. Тем самым осуществлялся переход от исходного пространства наблюдений размерности к экономному пространству признаков размерности 
( таблица 2).
Таблица 2. Потенциально полезные признаки термограммы
|
ЗНАЧЕНИЯ ПризнакОВ | ХАРАКТЕРНЫЕ ТОЧКИ ТЕРМОГРАММЫ | ||||||||
| A | B | C | D | E | F | G | H | J | |
 , c | 22 | 43 | 101 | 159 | 178 | 209 | 267 | 286 | 307 |
 , град C | 1200 | 1186 | 1138 | 1116 | 1119 | 1125 | 1108 | 1083 | 1050 |
 , град /c | -0.20 | -1.11 | -0.59 | 0.00 | 0.27 | 0.00 | -0.75 | -2.02 | -1.30 |
Именно эти признаки предложено использовать в качестве аргументов моделей для косвенной оценки химического состава и прогнозирования механических характеристик литейного чугуна.
Структурная и параметрическая идентификация таких моделей проводилось на основе использования двух выборок термограмм (обучающей и контрольной) с известными значениями технологических параметров. Построенные таким образом модели для условий Купянского литейного завода имели вид:
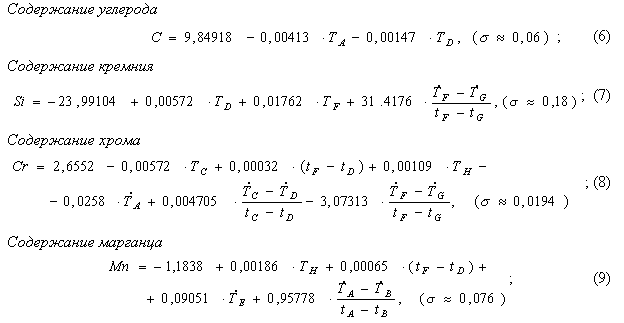
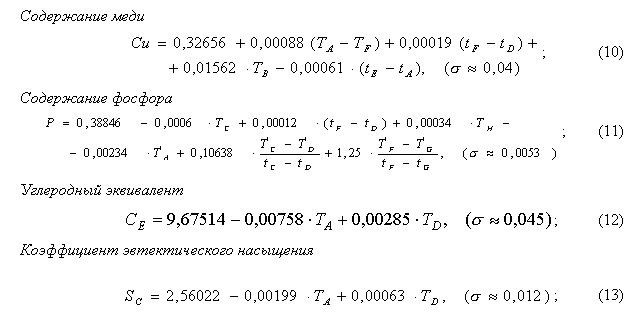
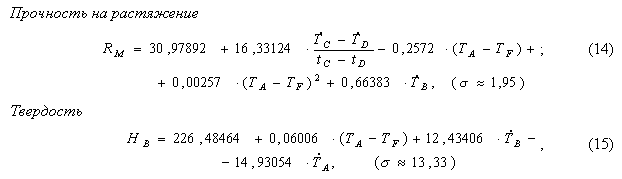
где 
- среднеквадратическое отклонение модельных и точных значений соответствующего параметра для наблюдений контрольной выборки.