Реферат: Об одном кулисно-рычажном механизме

(2.6)

Подставим из (2.3) выражение для в (2.6)

или, откуда имеем

(2.7)

Подставив (2.7) в (2.2), получим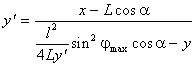 или

или

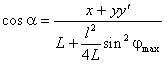(2.8)
Подставив из (2.8) выражение для в (2.7), получим

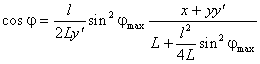(2.9)
Подставим (2.8) и (2.9) в (2.1), получим выражение:

,

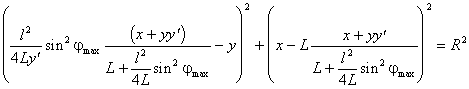в котором приведем к общему знаменателю выражения в скобках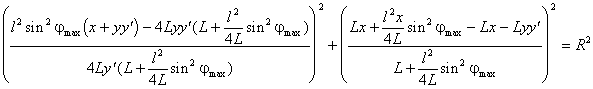

и затем сократим выражения в скобках,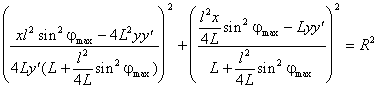

что приведет к окончательному виду дифференциального уравнения, определяющего форму направляющих

(2.10)
Если обозначить и , то уравнение (2.10) можно переписать как

(2.11)

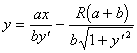(2.12)
Как известно, дифференциальное уравнение Лагранжа

приводится к уравнению в виде ;

переписав последнее относительно в виде (2.13)
и получаем линейное дифференциальное уравнение относительно.

Для уравнения (2.12) можно записать соотношения

, , , .

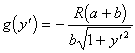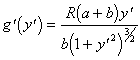Обозначим и запишем уравнение (2.13) как линейное дифференциальное уравнение относительно.

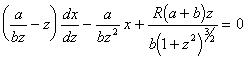(2.14)
Обозначим и перепишем уравнение (2.14) как линейное дифференциальное уравнение первого порядка,

или, после упрощения
(2.15)
Как известно, линейное дифференциальное уравнение первого порядка

при интегральном множителе имеет общее решение.

Для уравнения (2.15) можно записать

, .

Из /2/ имеем:

,

отсюда.