Реферат: Обобщенное золотое сечение и теория времени
Наибольшие отклонения ![]() получились для Солнца, Меркурия и Венеры, то есть для тел, расположенных в непосредственной близости к центру системы. По видимому, это объясняется тем, что Солнце, являясь генератором времени, искривляет время вокруг себя, что особенно заметно на малом расстоянии. Погрешности для остальных планет являются доказательством того, что они находится не точно на устойчивых орбитах, а в их окрестности.
получились для Солнца, Меркурия и Венеры, то есть для тел, расположенных в непосредственной близости к центру системы. По видимому, это объясняется тем, что Солнце, являясь генератором времени, искривляет время вокруг себя, что особенно заметно на малом расстоянии. Погрешности для остальных планет являются доказательством того, что они находится не точно на устойчивых орбитах, а в их окрестности.
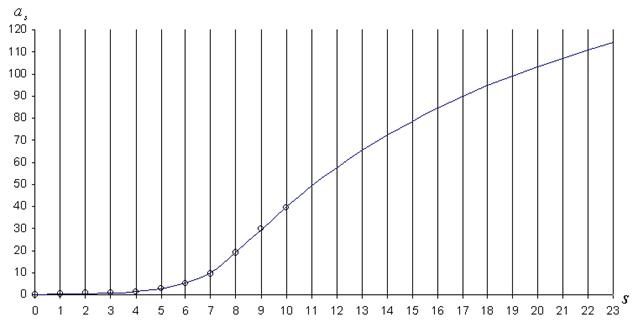
рис. 3
Из таблицы 3 и рисунка 3 видно, что, если гипотеза о связи ОЗС со значениями больших полуосей верна, за Плутоном должны существовать планеты с циклами около 346, 440, 530, 617, 699, 777 и так далее лет. Конечно, не на всех устойчивых орбитах обязательно существуют планеты, но опыт с Фаэтоном показывает, что свято место пусто не бывает и даже если там нет одной большой планеты, там должно находиться эквивалентное по массе количество малых тел. Автор взял на себя риск, исходя из мифологии, предложить имя одной из дальних (высших) планет. Кроме того, опираясь на некоторые данные, почерпнутые из древних текстов, можно предположить, что эклиптическая долгота планеты с циклом 440 лет, которую предлагается назвать Дхарма (в буддизме Дхарма - это общий универсальный мистериальный принцип взаимосвязи всех законов и явлений в мироздании, закон перемен, причинно-следственных изменений, универсальный вселенский закон причин и следствий), на середину 1996 года составляет примерно 43 градуса.
Обратим внимание, что фокус гиперболы лежит между значениями s =7 и s =8, то есть между Сатурном и Ураном, как раз на грани между планетами, видимыми невооруженным глазом, и планетами дальними, открытыми лишь относительно недавно. Кроме того, вблизи этой точки перегиба находится замечательный астероид Хирон (2060), который больше похож на планетоид, чем на осколок разрушенного небесного тела, как большинство других астероидов. Еще более интересно, что самая большая планета Солнечной системы - Юпитер, который иногда называют несостоявшейся звездой - попала почти точно в точку перегиба гиперболы (рис.2)! Не потому ли Юпитер "набрал" самый большой вес, что его орбита находится как раз на этом перегибе?
Из (13) также следует, что ![]() а.е.,
а.е., ![]()
Следующим этапом нашего анализа будет рассмотрение систем спутников планет, имеющее своей целью подтвердить или опровергнуть гипотезу о связи ОЗС с большими полуосями через функцию (13).
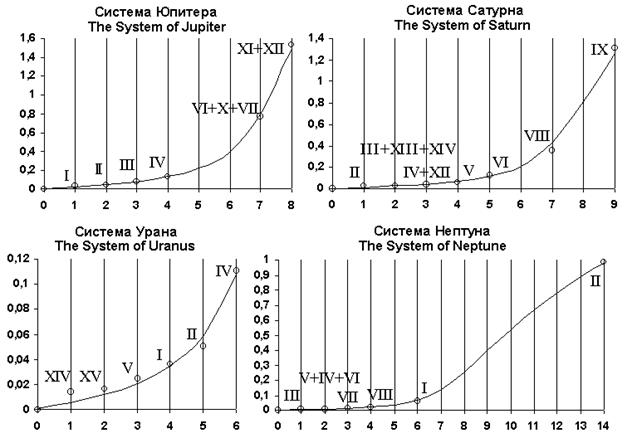
рис. 4
Наибольший интерес представляют системы спутников Юпитера, Сатурна, Урана и Нептуна. Скажем несколько слов о том, как проводился анализ. В первую очередь из рассмотрения пришлось исключить часть тел, имеющих неправильную форму, так как в большинстве своем они явно не укладывались ни в какую гладкую аппроксимацию. Также пришлось исключить из рассмотрения несколько весьма незначительных по размерам ближайших спутников в системах Юпитера, Сатурна и Урана. Предварительный анализ показал, что все системы спутников планет Солнечной системы хорошо аппроксимируются зависимостью (13), умноженной на поправочный коэффициент ![]() уникальный для каждой конкретной системы. Результаты этой аппроксимации для систем спутников Юпитера, Сатурна, Урана и Нептуна приведены на рисунке 4 (по оси абсцисс отложены значения s, по оси ординат - значения
уникальный для каждой конкретной системы. Результаты этой аппроксимации для систем спутников Юпитера, Сатурна, Урана и Нептуна приведены на рисунке 4 (по оси абсцисс отложены значения s, по оси ординат - значения ![]()
![]() ). Значения поправочных коэффициентов
). Значения поправочных коэффициентов![]() даны в таблице 4 и в виде графика на рисунке 5.
даны в таблице 4 и в виде графика на рисунке 5.
Приведенные на рисунке 4 графики позволяют сделать заключение, что общий вид и даже все параметры формулы (13) остаются практически без изменений в пределах всей Солнечной системы.
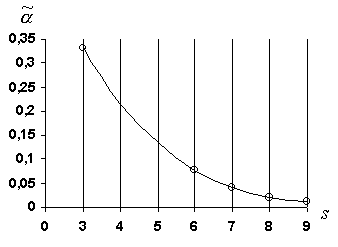
рис. 5
Таблица 4
| s | Планета | |
| 3 | Земля | 0,3315 |
| 6 | Юпитер | 0,0783 |
| 7 | Сатурн | 0,0428 |
| 8 | Уран | 0,0212 |
| 9 | Нептун | 0,0135 |
Из рисунка 5 и данных таблицы 4 очевидно, что коэффициент ![]() зависитобратно пропорционально от большой полуоси
зависитобратно пропорционально от большой полуоси ![]() :
:
![]()
То есть чем дальше от Солнца находится система, тем более она "сжата", тем стремительнее уменьшаются большие полуоси устойчивых орбит спутников при тех же значениях s . Противоположная картина наблюдается при приближении к Солнцу: здесь устойчивые орбиты спутников стремительно "раздуваются" и поэтому, к примеру, у Меркурия вообще не может быть спутников, так как первая ближайшая к нему устойчивая орбита спутника настолько велика, что любое тело, помещенное на нее, либо упадет на Солнце, либо переместиться на околосолнечную орбиту и станет еще одной малой планетой.
Отдельного рассмотрения заслуживает система спутников нашей с вами планеты - Земли. Коэффициент ![]() =0,3315 был выбран исключительно из того предположения, что идеальный цикл Луны должен составлять около 30 земных суток и Луна находится на орбите вокруг Земли соответствующей ОЗС при s =2.
=0,3315 был выбран исключительно из того предположения, что идеальный цикл Луны должен составлять около 30 земных суток и Луна находится на орбите вокруг Земли соответствующей ОЗС при s =2.
Цикл в 30 земных суток был выбран отнюдь не вследствие округления. Ведь градусная мера содержит в себе ровно 360 градусов, а древние календари - 12 месяцев по 30 дней. Такое совпадение не может быть случайным. Наиболее убедительным его объяснением является то, что идеальный (доисторический) цикл Луны составлял ровно 30 земных суток, а земной год длился ровно 360 земных дней (идеальный цикл Земли в таблице 3 получился равным 362 дня, что подтверждает эту гипотезу). Конечно, и сутки на Земле тогда должны были быть другими, но точную их продолжительность в те далекие времена установить пока не представляется возможным.
Соответствие орбиты Луны значению s =2 было принято, чтобы сохранить гладкость кривой на рисунке 5. При этом цикл первой устойчивой орбиты спутника Земли составил 9,5 дней, а третьей - 69 дней.
Система спутников Марса оказалась не подлежащей никакому анализу, так как оба его спутника являются телами неправильной формы и скорее всего это просто случайно захваченные Марсом астероиды, находящиеся вдали от устойчивых орбит. Попытки поместить один из спутников Марса на устойчивую орбиту приводили к потере гладкости кривой на рисунке 5.
Исходя из построенной аппроксимации, теоретически можно предположить существование спутника Венеры. К примеру, если принять для Венеры ![]() =0,55, то период обращения спутника по первой устойчивой орбите вокруг Венеры составит около 20 земных суток, а по второй - около 64 суток.
=0,55, то период обращения спутника по первой устойчивой орбите вокруг Венеры составит около 20 земных суток, а по второй - около 64 суток.
Итак, сделаем несколько заключительных выводов из всего вышеизложенного.
Ход времени и движение в пространстве неразрывно связаны друг с другом и по сути представляют собой один процесс.
"Постоянная" хода времени Козырева ![]() на самом деле равна абсолютной скорости движения системы, то есть скорости ее движения относительно фонового излучения Вселенной.
на самом деле равна абсолютной скорости движения системы, то есть скорости ее движения относительно фонового излучения Вселенной.
Для систем, которые на коротком промежутке времени можно считать замкнутыми, скорость хода времени относительно центра этой системы на протяжение короткого промежутка времени может быть принята за абсолютную.
Обобщенное Золотое Сечение (ОЗС) является универсальным ключом к анализу состояний динамического равновесия и может быть и должно быть применено для рассмотрения процесса хода времени, как процесса динамического равновесия свертки-развертки пространства.
Дискретный набор устойчивых соотношений прямой и обратной связи в причинно-следственном звене определяется по закону ОЗС.
Главные планеты Солнечной системы, также как и их спутники находятся вблизи устойчивых орбит, определяемых по закону ОЗС.
При удалении от центра Солнечной системы, системы спутников планет испытывают сжатие, которое выражается в уменьшении больших полуосей спутников для одного и того же "порога" ОЗС. Это происходит из-за возрастания расстояния до генератора времени - Солнца - и, вследствие этого, уменьшения плотности времени. Причем уменьшение плотности происходит обратно пропорционально расстоянию.
Так как классическое Золотое Сечение является, согласно большинству исследований, свойством живой материи, из этого следует, что Земля, Солнечная система и Вселенная в целом есть живой организм, живая самоорганизующаяся система, Самосознающий Воплощенный Абсолют.
Литература