Реферат: Обобщенные дискретные представления информации

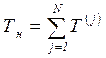. (2)

В результате анализа функции на интервале после окончания этого интервала формируется сообщение , которое передается в интервале представления. Обычно интервал представления выбирается равным:

, (3)

где - максимальный интервал корреляции, при

.

Координаты получаются как коэффициенты разложения сигнала в функциональный ряд по базисным функциям

. (4)

На приемной стороне по переданным координатам восстанавливается первичный сигнал

, (5)

а координаты на передающей стороне определяют как коэффициенты функционального ряда:

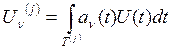, (6)

где - весовая функция, определенным образом связанная с .

Как следует из этого соотношения координата может быть представлена как результат фильтрации сигнала фильтра с импульсной характеристикой:

. (7)

Выбор лучшего обобщенного представления сводится к решению двух задач:

1. Выбор оптимального базиса .

2. Определение числа координат , обеспечивающих заданную

точность восстановления функции.

Оптимальные базисы, минимизирующие число координат при заданной точности восстановления, связаны с вероятностными характеристиками первичного сигнала. Они описываются громоздкими выражениями и на практике неудобны. Обычно используют универсальные базисы , применение которых не требует сложных устройств обработки и , в тоже время , достаточно эффективно. Такие базисы выбирают в классе ортогональных функций:

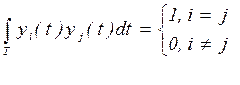. (8)

В качестве примера рассмотрим базисные функции в виде полиномов Лежандра и функций Уолша.

2. Представления сообщений с помощью полиномов Лежандра

Поместим начало отсчета времени в середину интервала представления:

Рисунок 2

Введем нормированное время

При таких обозначениях полиномы Лежандра задаются соотношением:

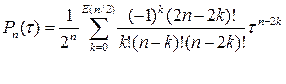, (9)