Реферат: Обратные задачи гравиметрии

Используя полученные в предыдущих параграфах уравнения, рассмотрим обратные задачи гравиметрии, т.е. найдем выражения для определения параметров и глубины залегания гравитирующих масс, сосредоточенных в телах простой геометрической формы.

Определение параметров и глубины залегания вертикального стержня. Изометрические аномалии (см. рис. 28, с. 126) можно аппроксимировать полем вертикального стержня или кругового цилиндра бесконечного простирания. Притяжение вертикального стержня с линейной массой l, рассредоточенной по всей его длине, определяется выражением:

. (V.35)

При x = 0 найдем максимальное значение Dgmax

.

Определим координату , в которой Dg равно половине

Dgmax :

.

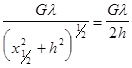Откуда

или

. (V.36)

Глубина залегания верхней кромки h1 и масса тела l могут быть найдены из следующих простых выражений:

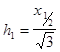; . (V.37)

Определение параметров залегания шара. Изометрические аномалии одного знака, замыкающие несколько большую площадь по сравнению с аномалиями от стержня (см. рис. 27, с. 126). можно аппроксимировать полем шара:

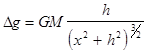. (V.38)

При x = 0

.

Найдем абсциссу , где :

,

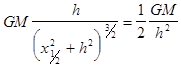откуда

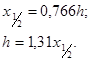(V.39)

Масса шара определяется из выражения:

. (V.40)

Если известна избыточная плотность , можно определить массу и радиус шара а.

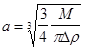, . (V.41)

Определение элементов залегания горизонтальной полуплоскости. Поле Dg, характерное для уступа, показано на рис. 29. Притяжение уступа определяется выражением:

, (V.42)

где r – поверхностная плотность.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--