Реферат: Обратные задачи гравиметрии

, (V.43)

откуда

.

Найдем координату , где ,

,

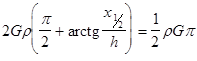откуда

. (V.44)

В случае уступа ограниченного простирания на глубину (рис. 29) при x = 0

, (V.45)

откуда

. (V.46)

При известной h1 по формуле (V.46) можно определить нижнюю кромку уступа h2, или, зная r, можно определить амплитуду h2 – h1.

Определение глубины залегания границы раздела плотности (контактной поверхности). Неглубокое расположение границы

Мохоровичича в океанах и известные средние значения плотности океанической коры и верхней мантии (рис. 31) позволяют при региональных исследованиях оценить глубину залегания границы М по следующей формуле притяжения бесконечного плоско-параллельного слоя:

.

Откуда, зная глубину h0 (например, по сейсмическим данным), можно определить h1 в любой другой точке профиля Dg:

. (V.47)

Рассмотренные выше приемы интерпретации гравитационных аномалий основаны на отыскании аналитической зависимости поля от координат и параметров возмущающих тел. Эти методы получили название методов характерных точек. Простота метода характерных точек делает его привлекательным для обработки массового материала. Однако он применим лишь для узкого класса тел правильной геометрической формы. Использование отдельных экстремальных точек, а не всей кривой Dg ведет к потере значительной части информации, заключенной в полученных аномалиях Dg. Поэтому применяемые другие методы интерпретации поля Dg особенно эффективны для тел произвольной геометрической формы.