Реферат: Однофакторний і двофакторний дисперсійний аналіз
де р-1= k2 — це число ступенів свободи для S2 2 , оскількигрупові середні варіюють відносно однієї загальної середньої ![]() .
.
Завдання виявлення впливу фактора на наслідки експериментуполягає в порівнянні виправлених дисперсій S 1 2 , S 2 2 . І справді, якщо досліджуваний фактор не впливає на значення ознаки X, то в цьому разі S1 2 і S2 2 можна розглядати як незалежні оцінки загальної дисперсії D. І навпаки, якщо відношення S1 2 і S2 2 істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.
Порівняння двох дисперсій ґрунтується на перевірці правильності нульової гіпотези: ![]() — про рівність дисперсій двох вибірок.
— про рівність дисперсій двох вибірок.
За статистичний критерій вибирається випадкова величина
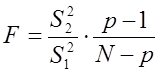 ,
,
що має розподіл Фішера-Снедекора з k1 = N- p, k2 = p-1 ступенями свободи
За значеннямиα ,k 1 = N - p , k 2 = p -1 , знаходимо критичнуточку.
Якщо F * ≤ Fkp , то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли F * > Fkp , то цим самимпідтверджується вплив фактора на ознаку X.
Результати спостережень та обчислення статистичних оцінокзручно подати в упорядкованому вигляді за допомогою табл. 2.
Таблиця 2


3. Двофакторний дисперсійний аналіз
Нехай необхідно визначити вплив двох факторів А і В на певну ознаку Х . Для цього необхідно, щоб дослід здійснювався при фіксованих рівнях факторів А і В , а також їх одночасній дії на ознаку. При цьому дослід здійснюватимемо п разів для кожного з рівнів факторів А і В .
Позначимо через xijk конкретне значення ознаки Х , якого вона набуває при і -му експерименті, j -му рівні фактора А і k -му рівні фактора В .
Результат експерименту зручно подати у вигляді таблиці, яка поділена на блоки, в кожному з яких враховується на певних рівнях факторів А і В їх вплив на конкретні значення ознаки X = xijk (табл.. 3).
Виходячи з даних табл.,
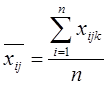
є середнім значенням ознаки Х для кожного блока;
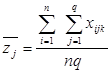 ,
, ![]()
є середнім значенням ознаки Х за стовпцями;
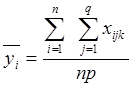 ,
, ![]()
є середнім значенням ознаки Х за рядками;
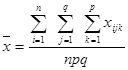
є загальною середньою ознакою Х ;
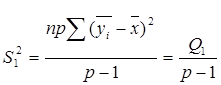
є виправленою дисперсією, яка зумовлена впливом фактора А на ознаку Х ;
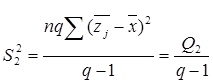
є виправленою дисперсією, яка зумовлена впливом фактора В на ознаку Х ;
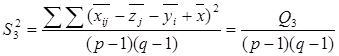
є виправленою дисперсією, яка зумовлена одночасним впливом на ознаку Х факторів А і В ;