Реферат: Одномерная оптимизация функций методом золотого сечения

d₀ = b₀ – a₀ .

После первого шага оптимизации получается новый интервал неопределенности – отрезок [a_1, b₁ ].

Можно показать, что точка x₁ делит этот отрезок в требуемом отношении, при этом

b₁ – x₁ = k₂ d₁ , d₁ = b₁ – a₁ .

Для этого проведем очевидные преобразования:

b₁ – x₁ = x₂ – x₁ = (b₀ – a₀ ) – (x₁ – a₀ ) – (b₀ – x₂ ) = d₀ – k₂ d₀ - k₂ d₀ = k₃ d₀ ,

d₁ = x₂ – a₀ = k₁ d₀ ,

b₁ – x₁ = k₃ (d₁ /k₁ ) = k₂ d₁ .

Вторая точка деления x₃ выбирается на таком же расстоянии от левой границы отрезка, т.е. x₃ – a₁ = k₂ d₁ .

И снова интервал неопределенности уменьшается до размера

d₂ = b₂ – a₂ = b₁ – x₃ = k₁ d₁ = kd₀ .

Используя полученные соотношения, можно записать координаты точек деления y и z отрезка [a_k , b_k ] на k +1 шаге оптимизации (y < z):

y = k₁ a_k + k₂ b_k ,

z = k₂ a_k + k₁ b_k .

При этом длина интервала неопределенности равна

d_k = b_k – a_k = kd₀ .

Процесс оптимизации заканчивается при выполнении условия d_k < ε. При этом проектный параметр оптимизации составляет a_k < x < b_k . Можно в качестве оптимального значения принять x = a_k (или x = b_k , или x = (a_k + b_k )/2 и т.п.).

Блок-схема алгоритма

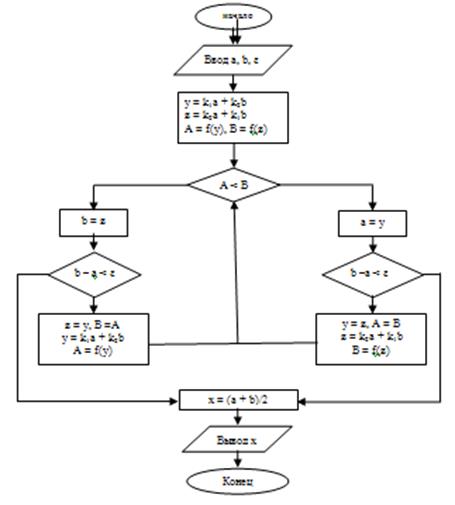
3. Программная часть

3.1 Текст программы в среде MatLab

А. Программа вычисления максимума:

function Maximum(a,b,eps)

%Maximum(a,b,eps) функция нахождения максимума функции f(x)

% методом "золотого сечения" на отрезке [a, b] с точностью eps.

% Функция f(x) задаётся в M-файле, находящимся в той же дирекктории.

% (!) Для правильной работы функции необходимо, чтоб a<b и

% искомое значение было б единствено на [a, b].

%--------------------------------------------