Реферат: Операторный метод анализа переходных колебаний в электрических цепях

Теорема запаздывания (оригинала) . Если , то , где — время запаздывания, т. е. запаздыванию оригинала на время соответствует умножение его изображения на экспоненциальный множитель .

Теорема смещения (изображения). Если , то , т. е. умножению оригинала на экспоненциальный множитель соответствует смещение его изображения на величину .

Решение задач прямого и обратного преобразований Лапласа существенно упрощаются в тех случаях, когда удается использовать справочные таблицы, которые содержат пары оригинал – изображение. Эти таблицы приводятся в справочниках.

Следует учесть, что при обратном преобразовании Лапласа полученные функции иногда не подходят под табличные. В этом случае используется разложение этой функции на простые дроби или в ряд с последующим применением обратного преобразования Лапласа.

Законы Кирхгофа и Ома в операторной форме

Возможность существенного упрощения решения задачи анализа колебаний в электрических цепях операторным методом основывается на том, что для -изображений колебаний формально верны законы Кирхгофа и Ома.

Действительно, согласно первому закону Кирхгофа:

Если обе части этого равенства подвергнуть преобразованию Лапласа, то оно переходит в равенство:

,

и следовательно, алгебраическая сумма -изображений токов в любом узле цепи равна нулю . Аналогично доказывается справедливость второго закона Кирхгофа для операторных напряжений в контуре:

.

При выводе закона Ома в операторной форме будем полагать, что реактивные элементы находятся при ННУ (конденсатор разряжен, через катушку индуктивности не протекает ток).

Рассмотрим соотношения в элементах электрических цепей.

Элемент резистивного сопротивления.

– операторное резистивное сопротивление,

– резистивная операторная проводимость.

Таким образом, операторное напряжение на резистивном сопротивлении равно произведению сопротивления на величину операторного тока.

Элемент индуктивности.

– операторное индуктивное сопротивление,

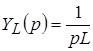– операторная индуктивная проводимость.

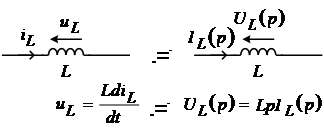
Следовательно, операторное напряжение на индуктивности равно произведению операторного индуктивного сопротивления на величину операторного тока.

Элемент емкости.

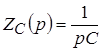– операторное емкостное сопротивление,

– операторная емкостная проводимость.

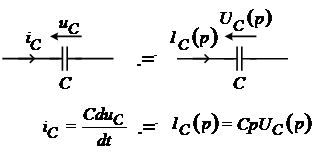
Операторное напряжение на емкости равно произведению операторного емкостного сопротивления на величину операторного тока.