Реферат: Операции с ценными бумагами

поскольку V представляет собой квадрат отклонения X отожидаемого значения т. Если нет отклонения, т.е. V = О, то и риска нет, чем больше V, тем больше риск. Возникает вопрос, какой риск описывается вели­чиной V. Это зависит от того, какому риску подвергаются инвесторы в период времени, по которому выбирается статистика.

Для моделирования портфеля важное значение будет иметь величи­на стандартного (среднеквадратичного) отклонения и ковариация двух случайных величин X₁ , X₂ :

V₁₂ = Е{( X₁ –т ₁ )( X₂ –т ₂ )}.

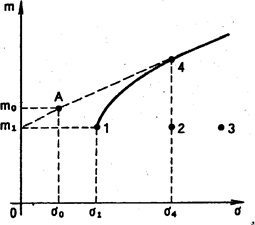
Рис. 1. Эффективные портфели

Предположим теперь, что имеется четыре различных портфеля, от­меченных на рис. 1 точками 7, 2,3,4 с координатами m_i (i = 1,2,3,4). Портфели, лежащие правее, имеют больший риск. Портфели, которым соответствуют точки, находящиеся выше, имеют больший эффект. Очевидно, что опытный инвестор будет действовать при выборе из двух пор­тфелей X_i и X_j следующим образом: он выберет X_i если выполняются одно из условий:

E(X_i )=E(X_j ), s (X_i ) < s (X_j );

E(X_j )>E(X_j ), s (X_i )= s (X_j ).

На графике этот выбор означает из первого и второго портфелей пер­вый (точка 1), из четвертого и второго - четвертый портфель (точка 4) В других случаях, когда

E(X_i )=E(X_j ), s (X_i ) < s (X_j )

каждый инвестор поступит соответственно своим предпочтениям и сво­ей склонности к риску. Однако если из всех возможных вариантов пор­тфелей выбрать все портфели, которые при каждом заданном уровне риска имеют максимальную ожидаемую эффективность (доходность) а при заданном уровне доходности имеют минимальный риск то это подмножество портфелей будет описываться кривой 1.- 4 (см рис 1)

Такие портфели называются эффективными, а кривая 7 - 4 представ­ляет множество эффективных портфелей. Остальные возможные порт­фели представляют собой множество неэффективных портфелей Из двух портфелей лучше тот, который находится ближе к множеству эффектив­ных портфелей. Среди эффективных портфелей инвестор должен выб­рать один, наиболее для него предпочтительный (оптимальный) На рис. 1 эффективными являются портфели 7 и 4, неэффективными - 2 и 3

Добавим теперь портфель с нулевым риском и гарантированной ожидаемой эффективностью m . Для нового множества допустимых портфелей граница эффективности теперь изменится и будет описывать­ся кривой m -4. Для этого множества портфелей портфель 1 перестал быть эффективным, так как портфель т имеет меньший риск чем пор­тфель 1 при одинаковой норме доходности.

Если инвестор согласен на риск в своем портфеле, то оптимальным для него будет портфель А со значениями риска ои ожидаемой эффек­тивности m Такой портфель можно сформировать, если взять долю s₀ / s₄ безрисковых вложений и долю (s₄ -s₀ )/ s₄ вложений из портфеля 4.

Практика показывает, что с увеличением количества видов ценных бумаг в портфеле уменьшается риск инвестиций. Это происходит пото­му, что в портфель включаются ценные бумаги, слабокоррелирован­ные между собой, только в этом случае возможно снижение риска Про­цедура включения в портфель различных видов ценных бумаг, имеющих низкий коэффициент корреляции, называется диверсификацией

При диверсификации риск портфеля снижается только до определен­ного уровня, ниже которого путем диверсификации риск уменьшить нельзя. Таким образом, риск представляет собой сумму диверсифициру­емого и недиверсифицируемого рисков. Диверсифицируемая часть риска представляет собой несистематический риск, а недиверсифицируемая - систематический.

Если задать желаемый для инвестора уровень доходности портфе­ля, то можно поставить задачу выбора такой структуры портфеля, ко­торая при заданном уровне доходности приводила бы к минимальному риску. Математическая постановка такой задачи впервые была сфор­мулирована в 1951 г. Г. Марковицем.

Для решения задачи Г. Марковица статистическими методами тре­буется большой объем данных о рынке ценных бумаг, накопленных за многие годы и отвечающих условиям представительности. На практи­ке, особенно на российском фондовом рынке, который еще только фор­мируется, такие данные получить очень трудно, а подчас и невозмож­но. В настоящее время появились различные эвристические методы для решения подобных задач, дающие псевдооптимальные решения, напри­мер различные генетические алгоритмы. Тем не менее традиционно для принятия решений о формировании портфеля пользуются моделью оценки финансовых активов (Capital Asset Pricing Model - САРМ), пред­ставляющей собой зависимость между эффективностью (доходностью) конкретной ценной бумаги и эффективностью рыночного портфеля (портфеля, содержащего все бумаги, находящиеся на рынке).

В САРМ-модели предполагается, что эффективность ценной бумаги Х линейно зависит от некоторого ведущего фактораF, описывающего эффективность рынка в целом, и в то же время на каждую j ценную бума­гу влияют и специфические для нее факторы, являющиеся случайными величинами е. Тогда

X_j = a _j + b _j F + e_j ,

где a _j и b _j - некоторые детерминированные величины, а коэффициент b _j отражает за­висимость эффективности бумаги от рыночной конъюнктуры, если b _j > О, то эффект бумаги аналогичен эффекту рынка, еслиb _j < 0, то эффектив­ность бумаги возрастает, когда эффективность рынка снижается.

Эта модель эффективности ценной бумаги носит название индекс­ной модели У. Шарпа.

Для характеристики конкретной ценной бумаги используются и дру­гие параметры. Если отсчитывать эффективность инвестиций в ценную бумагу от эффективности безрискового вклада r , то параметр

a _j = a _j - b _j r₀

представляет собой превышение эффективности ценной бумаги над без­рисковой эффективностью (можно считать это некоторой премией за риск). Если a _j < 0, то рыночная цена на эту бумагу завышена, и в бли­жайшем будущем она может понизиться; если же a _j > 0, то рыночная цена занижена, и в будущем вероятно ее повышение. Следовательно, при прочих равных условиях более предпочтительна бумага с a _j > 0.

На западных рынках значения а, b иR² регулярно рассчитываются для всех ценных бумаг и публикуются вместе с индексами. Пользуясь этой информацией, инвестор может сформировать собственный порт­фель ценных бумаг. На российском рынке профессионалы постепенно тоже начинают использовать а-, b- R² - анализ. Отдельные инвестици­онные институты рассчитывают а, b иR² .

2 .3. ДОХОДЫ ОТ ОПЕРАЦИЙ С ГОСУДАРСТВЕННЫМИ

ЦЕННЫМИ БУМАГАМИ

Основными видами государственных ценных бумаг на российском рын­ке являлись государственные краткосрочные бескупонные облигации (ГКО), облигации федерального займа с переменным купоном (ОФЗ-ПК) и облигации внутреннего валютного займа (ОВВЗ).

Рынок ГКО существовал с 1993 г., и за это время он превратился в самостоятельный сегмент фондового рынка. ГКО представляли собой дисконтную ценную бумагу, которая размещалась на аукционах и за­тем обращалась на .вторичном рынке. Обращение ГКО происходило в форме совершения сделок купли-продажи через Торговую систему -организацию, уполномоченную на основании договора с Банком Рос­сии обеспечивать процедуру заключения сделок купли-продажи ГКО.

Погашение ГКО производилось в безналичной форме путем пере­числения их владельцам номинальной стоимости облигаций на момент погашения (сейчас номинал облигации - 1000 руб.). Разница между ценой погашения (номиналом) и ценой приобретения на аукционе ил вторичных торгах представляет доход инвестора.

Относительным показателем выгодности инвестирования средств! ГКО являлась доходность, которая рассчитывалась как отношение полученного дохода к сумме вложенных средств, приведенное к годовом периоду. Для расчета доходности ГКО использовались следующие показатели:

1) минимальная цена аукциона (цена отсечения) наименьшая цен облигации, начиная с которой удовлетворяются конкурентные заявки на аукционе;

2) средневзвешенная цена, равная отношению оборота ГКО к суммарному количеству облигаций, участвующих в сделках:

k k

P = å P_i n_i / å n _i

i=1 i=1

где P_i - цена участвующих в сделке облигаций i-ro вида (для аукциона значение P_i , не ниже цены отсечения);

n _i - количество участвующих в сделке облигаций i-го вида;