Реферат: Определение динамических характеристик системы

Если помеха не коррелирована с управляющим воздействием , что чаще всего и бывает, то последнее слагаемое равно нулю и

. (4)

Полученное выражение представляет собой интеграл свертки. Оно аналогично выражению (1). Если рассматривать корреляционную функцию как входное воздействие, а взаимную корреляционную функцию – как выходной процесс, то указанная аналогия станет очевидной.

Заметим, что в окончательном выражении (4) не фигурируют ни характеристики помехи, ни импульсная переходная функция по помехе. Не отражен даже сам факт наличия помехи.

Если бы вывод этого выражения был основан на использовании выражения (1), а не (2), т.е. в предположении, что помеха отсутствует, то и тогда было бы получено выражение связи (4).

Этим не исчерпываются замечательные свойства полученного выражения. Предположим, что на входе системы действует «белый шум», т.е. . Тогда по основному свойству d - функции

.

Другими словами, если на вход системы подавать «белый шум», то взаимно корреляционная функция будет численно равна импульсной переходной функции системы.

Это чисто теоретический результат, но он имеет большое практическое значение. Как известно, «белый шум» - это абстрактное математическое понятие, идеализация случайного процесса, спектральная плотность которого одинакова для любой частоты. Такого процесса в природе не существует: для его генерации потребовался бы источник бесконечно большой мощности. Однако к такой идеализации прибегают всякий раз, когда изменением спектральной плотности в полосе пропускания системы можно пренебречь.

Но даже с учетом этого обстоятельства полученный результат имеет большое значение, потому что чем ближе спектральная плотность к «белому шуму», тем ближе взаимная корреляционная функция к импульсной переходной функции.

2 Определение импульсной переходной функции объекта по статистическим характеристикам

Если входной процесс не может считаться «белым шумом», для определения импульсной переходной функции необходимо решить интегральное уравнение (4).

Рассчитывать на аналитическое решение данного уравнения после экспериментального определения корреляционных функций и в подавляюще большинстве случаев не приходится. Для этого применяются численные методы.

Для решения различного рода уравнений численными методами необходима дискретизация задачи. В данном случае для этого достаточно заменить интеграл в выражении (4) конечной суммой.

При вычислении интеграла по формуле прямоугольников это происходит естественным образом. Для применения упомянутой формулы интервал интегрирования разбивают на достаточно малые подинтервалы длиной Т , на каждом из которых подынтегральная функция мало изменяется.

В качестве интервала интегрирования возьмем интервал (0, L). Нижняя граница определяется условием физической осуществимости: при отрицательных значениях аргумента импульсная функция равна нулю, а конечный верхний предел определяется условием устойчивости системы: импульсная переходная функция устойчивой системы должна стремиться к нулю.

Следовательно, найдется такое значение аргумента импульсной переходной функции L, что при больших значениях она пренебрежимо мала. Далее, разобьем интервал (0, L) на N одинаковых по длине подинтервалов, каждый из которых имеет длину T .

После этого уравнение (4) можно с достаточной степенью точности представить в виде суммы

.

Полагая , получим систему N уравнений относительно N неизвестных

. (5)

Обозначив , , и учитывая четность корреляционной функции , полученную систему уравнений можно записать в развернутом

;

;

………………………………….…….

.

или матричном виде

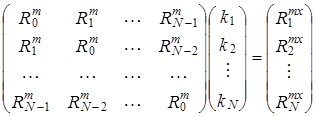
В результате решения этой системы уравнений можно получить значения импульсной переходной функции при .