Реферат: Определение динамических характеристик системы

Из уравнения связи между входным и выходным процессами в детерминированном случае также можно получить систему уравнений относительно значений импульсной переходной функции.

Действительно, связь между входом и выходом во временной области описывается уравнением свертки (1). Оно до сих пор рассматривалось как выражение выходной координаты через входную, как интегральный оператор, который ставит входному процессу в соответствие некоторый выходной процесс.

Описание импульсной переходной функции и входного процесса в этом случае должно быть известно.

Если же известными являются другие две компоненты из трех: входного и выходного процесса и требуется определить импульсную переходную характеристику, то на данное выражение следует смотреть как на интегральное уравнение.

Оно может быть решено и в результате получено значение импульсной переходной функции.

Действительно, повторив рассуждения по выводу уравнения (5) из уравнения (4), из уравнения (1) получим уравнение

.

При получим отсюда систему N уравнений относительно N неизвестных . Обозначив , , , полученную систему уравнений можно записать в виде

.

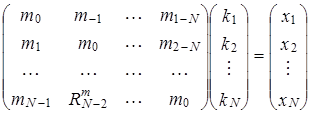Различие между двумя этими системами уравнений не только в том, что в одном случае матрица системы уравнений симметричная, а в другом – нет. Основное различие в степени влияния шумов на результат вычислений.

Если шумы значительны, то ошибки при определении импульсной переходной функции по детерминированным характеристикам могут быть очень велики.

В то же время, если шумы (помехи) при определении соответствия межу входом и выходом некоррелированы с входным воздействием, то они могут иметь любую интенсивность.

Точность результата вычислений от этого не изменится, но при этом необходимо оперировать не значениями самих сигналов, а их корреляционными функциями.

Если же помехи отсутствуют, то нет необходимости прибегать к статистическим методами. В детерминистическом случае наряду с рассмотренным только что подходом к определению импульсной переходной функции существует еще один, обладающий определенными достоинствами по сравнению с только что рассмотренным.

Они связаны с большей простотой уравнения, которое необходимо решать для определения дискретных значений импульсной переходной функции.

Как уже отмечалось, связь между входным и выходным процессами выражается не только интегралом свертки (1), но и интегралом

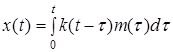
В свое время были даны доказательства возможности замены переменного верхнего предела бесконечным значением. В данном случае в этом нет необходимости. Наоборот, всякое сужение области интегрирования приводит к упрощению системы уравнений, которую необходимо решать.

Заменим интеграл конечной суммой точно так же, как это делалось ранее. Получим

.

Здесь так же все процессы рассматриваются в дискретные моменты времени . Полученное выражение здесь также можно рассматривать как систему N уравнений относительно N неизвестных , но лучше рассматривать его как рекуррентное уравнение.

Обозначив , , , полученную систему уравнений для различных, последовательно увеличивающихся значениях n можно записать в виде

;

;

;

………………………….

Отсюда

;

;
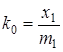
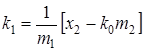