Реферат: Определители Решение систем линейных уравнений

В случае, когда система имеет единственное решение, это решение можно найти с помощью определителей второго порядка.

ОПРЕДЕЛЕНИЕ 5 . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы.

Обозначим определитель системы D.

D = .

В столбцах определителя D стоят коэффициенты соответственно при х ₁ и при_, х ₂ .

Введем два д о п о л н и т е л ь н ы х о п р е д е л и т е л я , которые получаются из определителя системы заменой одного из столбцов столбцом свободных членов:

D₁ = 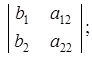D₂ = .

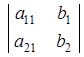Рассмотрим без доказательства следующую теорему:

ТЕОРЕМА КРАМЕРА (для случая n = 2)

Если определитель D системы (3) отличен от нуля (D¹ 0), то система имеет единственное решение, которое находится по формулам:

(4)

Формулы (4) называются формулами Крамера.

ПРИМЕР. Решить систему по правилу Крамера.

.

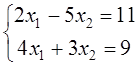
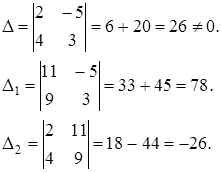
Ответ: х ₁ = 3; х ₂ = -1

2. Система трех линейных уравнений с тремя неизвестными:

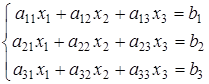(5)

В случае единственного решения систему (5) можно решить с помощью определителей третьего порядка.

Определитель системы D имеет вид:

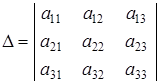
Введем три дополнительных определителя:

.

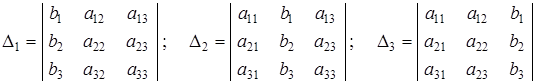Аналогично формулируется теорема.

ТЕОРЕМА КРАМЕРА (для случая n = 3)

Если определитель D системы (5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:

(6)

Формулы ( 6 ) – это формулы Крамера.

ЗАМЕЧАНИЕ. Г. Крамер (1704 – 1752) – швейцарский математик.

Заметим, что теорема Крамера применима, когда число уравнений равно числу неизвестных и когда определитель системы D отличен от нуля.

Если определитель системы равен нулю, то в этом случае система может либо не иметь решений, либо иметь бесчисленное множество решений. Эти случаи исследуются особо, с ними можно подробно познакомиться в рекомендуемой литературе.

Отметим только один случай:

Если определитель системы равен нулю (D = 0), а хотя бы один из дополнительных определителей отличен от нуля, то система решений не имеет (т.е. является несовместной).

Теорему Крамера можно обобщать для системы n линейных уравнений с n неизвестными.

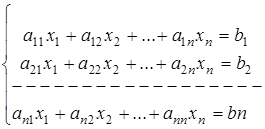
Если 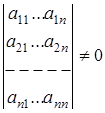, то единственное решение системы находится по

формулам Крамера: