Реферат: Оптимизация производственной программы АПП и управление запасами ресурсов

Аналитические методы абсолютно точны. Они дают возможность для точной количественной оценки излишков имеющихся ресурсов.

Приведем задачу к канонической форме:

2,1Х1 + Х3 = 1250;

Х1 + 0,54Х2 + Х4 = 1000;

0,6Х2 + Х5 = 132;

Х1 + Х6 = 580.

Дополнительные переменные Х3, Х4и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае - излишний запас).

3.1. Решение задачи аналитическим методом
с использованием Excel

Пусть имеется математическая модель:

2,1Х1 ≤ 1250;

Х1 + 0,54Х2 ≤ 1000;

0,6Х2 ≤ 132;

Х1 ≤ 580;

Х1 ≥ 0, Х2 ≥ 0;

F = 40Х1 + 10Х2 ®max

Для решения данной задачи необходимо в ячейки С10- D 13 записать коэффициенты математической модели, в G 10- G 14 правые части ограничений, а в C 3 и D 3 – коэффициенты целевой функции (рис. 1).

КРС	Птица	Прибыль	max
Значение	505	0	20190,47619
Коэффициенты ЦФ	40	10
Ограничения
Расход	Запас
Вид ресурса	Левая часть	Правая часть	Остаток	Остаток,%
Силос	2,1	0	1060	<=	1250	190	15,2
комбикорм	1	0,54	504,7619048	<=	1000	495,238	49,5
Трудовые	10,5	2,5	5300	<=	5300	0	0,0
Зерно	0	0,6	0	<=	132	132	100,0
Выпас	1	0	504,7619048	<=	580	75,2381	13,0

Рисунок 1. Пример формирования исходных данных

Далее следует щелкнуть мышкой на Сервис , а затем Поиск решения . На экране монитора появляется окно, изображенное на рисунке 2.

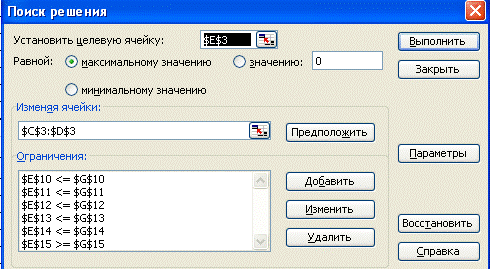
Рисунок 2. Пример экрана Поиск решения

После нажатия на Выполнить появляется окно, изображенное на рис. 3, где можно посмотреть результаты и исследовать на устойчивость и пределы.

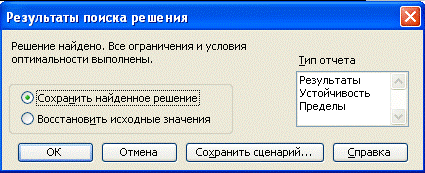
Рисунок3. Результаты поиска решения

После ОК на экране появляются результаты решения, пример которых приведен на рис. 4.

КРС	Птица	Прибыль	max
Значение	505	0	20190,47619
Коэффициенты ЦФ	40	10
Ограничения
Расход	Запас
Вид ресурса	Левая часть	Правая часть	Остаток	Остаток,%
Силос	2,1	0	1060	<=	1250	190	15,2
комбикорм	1	0,54	504,7619048	<=	1000	495,238	49,5
Трудовые	10,5	2,5	5300	<=	5300	0	0,0
Зерно	0	0,6	0	<=	132	132	100,0
Выпас	1	0	504,7619048	<=	580	75,2381	13,0

Рисунок 4. Пример окончательного решения

Результаты расчетов Х1 и Х2 находятся в ячейках С3 и D 3 . Целевая функция - в ячейке E 3 . Столбец «Левая часть » характеризует фактическое использование ресурсов. «Остаток » определяется разностью между имеющимися запасами (Правая часть ) и их фактическим использованием (Левая часть ).

После завершения каждой итерации расчета результаты целесообразно сохранять под новым именем.

Для выполнения каждой последующей итерации достаточно лишь в столбце F изменить числа, характеризующие запасы ресурсов.

Каждая итерация должна завершаться финансовой проверкой, которая состоит в том, что деньги, вложенные в ресурсы, должны оставаться неизменными. Кроме того, необходимо следить за тем, чтобы целевая функция после каждой итерации увеличивалась. Если это не происходит, значит, закуплен не дефицитный ресурс или избыточный ресурс продан в слишком большом количестве и стал дефицитным.

4. Графический метод решения задачи

Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Для каждого аналитического метода решения задачи существует соответствующий ему графический метод.

4.1. Решение задачи графическим методом
с помощью Excel

Программа MicrosoftExcel -2000 предназначена для работы с электронными таблицами, позволяющими собирать, анализировать и представлять количественную информацию в автоматическом режиме. Файл, создаваемый в Excel, называется рабочей книгой.

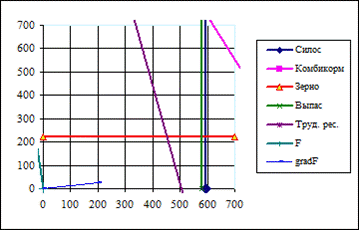
Для изображения линий, характеризующих ограничения, координаты соответствующих точек следует записать так, как это показано на рис. 5.

В ячейках M 7 – M 11 – правые части ограничений – запасы ресурсов. В столбце В задаются значения Х1 . Координаты Х2 вычисляются по уравнениям, характеризующим ограничения.

Ресурс	Х2
	Х1	Силос	Комбик	Зерно	Выпас	Труд.рес.	F	gradF
Силос	595,2381	0
	595,2381	2900
Комбикорм	0	1851,852
	800	370,3704
Зерно	0	220
	700	220
Выпас	580	0
	580	2900
Труд.рес.	0	2120
	700	-820
F	0	0
	-25	200
gradF	0	0
	200	25

Рисунок 5. Пример записи исходных данных

Так как в ячейках M 7 – M 11 находятся значения, характеризующие запасы ресурсов, то при каждом изменении запасов ресурсов, мы вводим в эти ячейки обновленные данные и получаем решение графическим методом.

Ресурс	Х2
	Х1	Силос	Комбик	Зерно	Выпас	Труд.рес.	F	gradF
Силос	595,2381	0
	595,2381	2900
Комбикорм	0	1851,852
	800	370,3704	Запасы ресурсов
Зерно	0	220	Силос	1250
	700	220	Комбикорм	1000
Выпас	580	0	Зерно	132
	580	2900	Выпас	580
Труд.рес.	0	2120	Труд.рес.	5300
	700	-820
F	0	0
	-25	200
gradF	0	0
	200	25

Рисунок 6. Пример окончательного решения графическим методом

5. Решение задачи

5.1 Вторая итерация

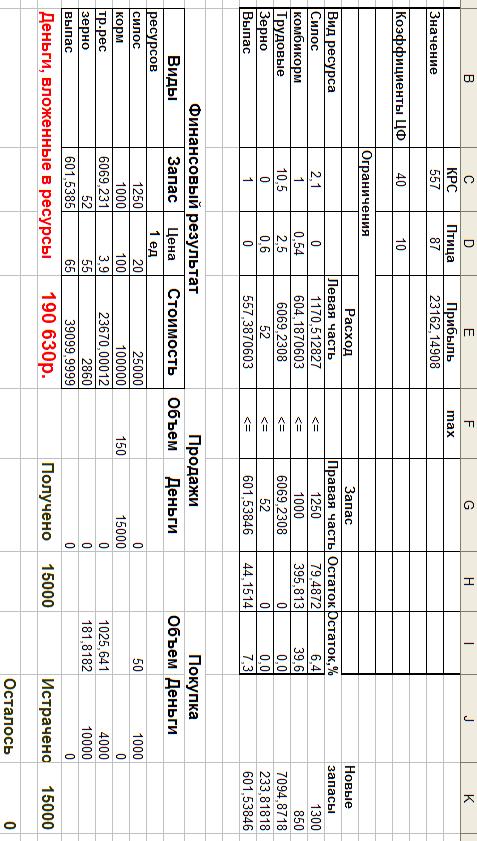
5.2 Третья итерация

Четвертая итерация

Пятая итерация

Шестая итерация

Седьмая итерация

6. Решение задачи в условиях
узкой специализации

Узкая специализация позволяет улучшить качество и увеличить производительность за счет более простой типовой схемы движения предметов труда.

Определим рентабельность производства крупного рогатого скота и птицы как частное от деления прибыли на затраты на производство единицы продукции. Так как целесообразно производить более рентабельный продукт.

В данной задаче рентабельность производства крупного рогатого скота составляет:

R_КРС =(40/(2,1*20+1*100+1*65+10,5*3,9)*100=16%.

Рентабельность производства птицы составляет: