Реферат: Оптимизация структуры стохастического графа c переменной интенсивностью выполнения работ
Задача распределения ресурсов (нескладируемого типа) на cтохастических сетях (параллельные проекты) сформулирована как обусловленная переменной структурой графа. Предложенный метод решения обеспечивает получение экстремального графа для случая, когда каждая работа многопроектной разработки может выполняться с переменной интенсивностью использования ресурсов. Принципиально новый подход к решению задачи распределения ресурсов на сетях позволяет совершить качественный скачок в области математического обеспечения автоматизированных систем управления, так как создаются предпосылки для использования всех достижений сетевого планирования при управлении ресурсами, которые выполняют параллельные проекты.
1. Введение.
Все известные теории решения задач распределения ресурсов на сетях базируются на комбинаторике, которая приводит либо к анализу бесконечного числа вариантов, либо к привлечению эвристики. Прежде чем приступить к распределению ресурсов производят расчет сетевых графиков, каждый из которых построен на основании технологии и принятой организации работ по каждому проекту. Затем полученные таким образом показатели, а также критические пути используются в качестве подсобного инструмента с целью обеспечения работ ресурсами и получения расписания их выполнения в планируруемом периоде времени [1, 2, 3, 4, 5].
Необоснованность традиционного решения можно легко показать на примерах, иллюстрирющих возникающие при этом парадоксы[6], причина которых состоит в том, что при распределении ресурсов между работами возникают связи по использованию одного и того же ресурса. Поскольку возможны различные варианты перехода каждой единицы ресурса с одной работы на другую, то задача нахождения ресурсных связей многовариантна ( обусловлена переменной структурой графа ). Каждый вариант распределения ресурсов определяет топологию сетевой модели, которая характеризуется своими параметрами. Оптимальный вариант определяет оптимальную топологию сетевой модели согласно выбранному критерию. Следовательно при традиционном подходе к решению задачи распределения ресурсов на сетях трудаемкая работа, требующая участия коллек-тива и затрачиваемая на составление сетевых графиков, а также их расчета на ЭВМ, выполняется впустую. Кроме того, поскольку конечной целью при этом является получение расписания выполнения работ, то сетевая модель вообще выпадает из управления [7, 8, 9, ]. Неудачные попытки ввести в сетевое планирование нескладируемой ресурс привели к затуханию интереса к данному направлению. В настоящее время в научной литературе внимание в основном уделяется задачам загрузки оборудования и построение расписаний [10, 11, 12, 13, 14, 15].
2. Постановка.
Задачу распределения ресурсов на сетях, базой которой является принципиально новая теория, сформулируем на примере проектной организации. Тематический план проектной организации содержит как новые проекты, так и переходящие из плана предыдущего года. Каждый проект представлен в виде элементарных составляющих работ с указанием множества условий ( под множеством условий понимаются другие работы того же самого проекта, результаты каждой из которых, согласно технологии проектирования, необходимы для того, чтобы начать данную).
При этом каждый проект может содержать такие работы, от результатов которых зависит дальнейшее развертывание проектирования проекта. Иначе говоря, нельзя полностью определить технологию проектирования проекта, поскольку результат некоторых работ влияет на последующий ход его реализации. Такие работы мы будем называть решающим результатом. В одном проекте может быть несколько решающих результатов.
Введение решающих работ позволяет принимать в расчет альтернативы, которые возникают на некоторых этапах реализации проекта [16]. Каждой альтернативе приписана априорная вероятность. Каждая работа помимо взаимоcвязи с другими работами согласно технологии проектирования характеризуется видом ресурса, которым она может выполняться, а также трудоемкостью. Каждый ресурс специализированного подразделения характеризуется его наличием и пределами потребления данного ресурса на различных работах. Требуется определить стохастическую сетевую модель, отображающую многопроектную разработку с учетом ресурсов.
Введем условные обозначения: ![]() число проектов;
число проектов; ![]() число различных видов ресурсов , обеспечивающих выполнение многопроектной разработки;
число различных видов ресурсов , обеспечивающих выполнение многопроектной разработки; ![]() продолжительность критического пути m-го проекта в сетевом графике без учета ресурсов,
продолжительность критического пути m-го проекта в сетевом графике без учета ресурсов, ![]()
![]() продолжительность самой длинной цепочки работ, выполняемых i-ым видом ресурса,
продолжительность самой длинной цепочки работ, выполняемых i-ым видом ресурса, ![]()
![]() множество работ многопроектной разработки (данное множество включает работы всех проектов, которые задаются общим списком);
множество работ многопроектной разработки (данное множество включает работы всех проектов, которые задаются общим списком);
![]() код j-й работы,
код j-й работы, ![]()
![]() весовой коэффициент j-й работы,
весовой коэффициент j-й работы, ![]()
![]() вид ресурса, которым может выполняться j-я работа,
вид ресурса, которым может выполняться j-я работа, ![]()
![]() максимально возможное число ресурсов для j-й работы,
максимально возможное число ресурсов для j-й работы,![]()
![]() трудоемкость j-й работы,
трудоемкость j-й работы, ![]()
![]() планируемое число ресурсов на j-ю работу,
планируемое число ресурсов на j-ю работу, ![]()
![]() множество технологических условий для j-й работы,
множество технологических условий для j-й работы, ![]()
![]() множество ресурсных условий (данное множество включает работы, c каждой из которых ресурсы переходят на выполнение j-й работы,
множество ресурсных условий (данное множество включает работы, c каждой из которых ресурсы переходят на выполнение j-й работы, ![]() );
);![]() код q-го условия для j-й работы,
код q-го условия для j-й работы, ![]()
![]()
![]() срок начала j-й работы,
срок начала j-й работы, ![]()
![]() срок окончания q-го условия для j-й работы,
срок окончания q-го условия для j-й работы, ![]()
![]() множество работ многопроектной разработки, каждая из которых выполняется i-м видом ресурса в к-ю единицу времени,
множество работ многопроектной разработки, каждая из которых выполняется i-м видом ресурса в к-ю единицу времени, ![]()
![]()
![]()
![]() число единиц ресурса i-го вида,
число единиц ресурса i-го вида, ![]()
![]() число работ множества
число работ множества ![]()
Прежде чем дать математическую формулировку задачи, введем определения:
1. Под ресурсным графом мы понимаем сетевую модель, отображающую многопроектную разработку с учетом ресурсов.
2. Под установлением между работами связей по ресурсам мы понимаем указание для j-й работы множества ресурсных условий Zj , ![]()
3. Путь, имеющий продолжительность Tm , ![]()
![]() мы называем критическим путем сетевого графика для m-го проекта без учета ресурсов.
мы называем критическим путем сетевого графика для m-го проекта без учета ресурсов.
4. Путь, имеющий продолжительность ![]() мы называем критическим путем сетевой модели многопроектной разработки без учета ресурсов. Сетевая модель в данном случае состоит из совокупности сетевых графиков.
мы называем критическим путем сетевой модели многопроектной разработки без учета ресурсов. Сетевая модель в данном случае состоит из совокупности сетевых графиков.
5. Путь ресурсного графа, имеющий продолжительность ![]() , мы называем. критическим.
, мы называем. критическим.
. . ![]() V(t0 )
V(t0 )![]() известно( состояние системы в момент времени t0 ).
известно( состояние системы в момент времени t0 ).
(1) 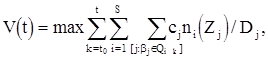 для любого
для любого ![]()
(2) ![]()
![]()
![]()
(3) ![]()
(4) ![]() целое,
целое, ![]()
(5) ![]()
При заданном начальном состоянии системы V(t0 ) в момент времени t0 необходимо найти в области, определяемой ограничениями: (2)![]() (5), оптимальную траекторию движения(под оптимальной траекторией движения системы мы понимаем экстремальный граф, параметры которого для любого k
(5), оптимальную траекторию движения(под оптимальной траекторией движения системы мы понимаем экстремальный граф, параметры которого для любого k![]() обеспечивают максимальное значение функции (1)).
обеспечивают максимальное значение функции (1)).
Положение j-й работы в графе (1) определяется указанием множества ресурсных условий Zj , ![]() . Граф(1) для каждого решающего результата включает только одну альтернативу.
. Граф(1) для каждого решающего результата включает только одну альтернативу.
. Обоснованность критерия (1) следует из определения ресурсов нескладируемого типа, которые отпускаются порциями ?квантами¦.Для них характерно то, что неиспользованная или неэффективно использованная часть каждой порции в каждый момент времени пропадает и не переносится на другое время.
Физически критерий (1) означает, что число выполненных работ с учетом их весовых коэффициентов за любой интервал времени должно быть максимальным. Согласно ограничению (2) у-я работа не может начаться раньше окончания своих условий. Для начала любой работы необходимо, чтобы к данному моменту времени были выполнены технологические условия а также свободны ресурсы, обеспечивающие ее выполнение. Ресурсы могут переходить с других работ, которые также для данной работы являются условиями
Система функционирует в дискретном времени и ее состояние в каждый момент определяется набором числовых параметров: ni , Zj , ![]()
Принимаются следующие допущения: 1) каждая работа может выполняться с переменной интенсивностью использования ресурсов; 2) выполнение работ может прерываться, даже если они не закончены. Они будут завершены позднее.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--