Реферат: Организация информации
15,375 = 0 1000.0000.00010. 1110.1100.0000.0000. … 00002 = 402ЕС0000000000016 .
Источник: [5].
Особенности плавающей арифметики могут существенно влиять на результаты расчётов, вплоть до того, что погрешность может сделать невозможным получение какого-либо результата вообще, поэтому знание деталей реализации арифметики плавающих чисел является необходимым для программистов.
Пример
Существует особая характеристика плавающей арифметики – машинное эпсилон. Это число, которое определяется как
![]() .
.
Для плавающего числа единичной точности (по IEEE стандарту):
![]() .
.
Это значит, если написать программу на языке BASIC:
a=1.2
b=1.e-7
printa+b
то результат, который выдаст программа, будет равен 1.2.
Поэтому программы, учитывающие особенности плавающей арифметики могут трактовать все числа, меньшие, чем машинное эпсилон, практически равными нулю.
Цифровое представление изображений
Под изображением будем понимать прямоугольную область, закрашенную непрерывно изменяющимся цветом. Поэтому для представления изображений в целых числах необходимо отдельно дискретизировать прямоугольную область и цвет.
Для описания области она разбивается на множество точечных элементов – пикселов [pixel]. Само множество называется растром [bitmap, dotmatrix, raster] (см. рис. 1.3), а изображения, которые формируются на основе растра, называются растровыми.
 |
???.4. ????????????? ??????? ???????????
Число пикселов называется разрешением [resolution]. Часто встречаются значения 640х480, 800х600, 1024х768, 1280х1024. Каждый пиксел нумеруется, начиная с нуля слева направо и сверху вниз.
Для представления цвета используются цветовые модели. Цветовая модель [colormodel] это правило, по которому может быть вычислен цвет. Самая простая цветовая модель – битовая. В ней для описания цвета каждого пиксела (чёрного или белого) используется всего один бит. Для представления полноцветных изображений используются несколько более сложных моделей. Известно, что любой цвет может быть представлен как сумма трёх основных цветов: красного, зелёного и синего. Если интенсивность каждого цвета представить числом, то любой цвет будет выражаться через набор из трёх чисел. Так определяется наиболее известная цветовая RGB-модель. На каждое число отводится один байт. Так можно представить 224 цвета, то есть примерно 16,7 млн. цветов. Белый цвет в этой модели представляется как (1,1,1), чёрный – (0,0,0), красный (1,0,0), синий (0,0,1). Жёлтый цвет является комбинацией красного и зелёного и потому представляется как (1,1,0).
Пример
Пусть имеется изображение вида
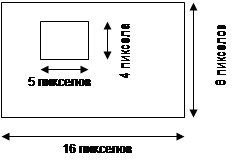 |
????? ???????, ??? ????? ???? ?????????????? ?????, ? ?????? ? ????????, ????? ? ??????????? ?????? ????? ??????????? ???????????? ? ????:
0000000000000000
0000000000000000
0000111110000000
0000100010000000
0000100010000000
0000111110000000
0000000000000000
0000000000000000
В шестнадцатеричном виде этот двоичный набор будет выглядеть так:
00 00 00 00 0F 80 08 80 08 80 0F 80 00 00 00 00