Реферат: Осесиметричні коливання дискретно підкріплених оболонкових елементів конструкцій на пружній основі при імпульсних навантаженнях

У другому розділі детально викладено постановки задач осесиметричних та неосесиметричних коливань підкріплених оболонок обертання з врахуванням зовнішнього середовища. Покладалось, що напружено-деформований стан неоднорідної пружної структури може бути визначений в рамках геометрично нелінійної теорії оболонок і стержнів типу Тимошенка. Деформований стан гладкої оболонки визначається через компоненти узагальненого вектора переміщень серединної поверхні –. Деформований стан ребра, направленого вздовж осі , визначається вектором переміщення лінії центра ваги поперечного зрізу.

Деформаційні співвідношення для обшивки визначаються згідно формул

,... , (1)

Покладається, що підкріплюючі ребра жорстко з’єднані з гладкою оболонкою. Умови контакту оболонка – j-те ребро приймаються у вигляді

.…. (2)

Для виводу рівнянь коливань підкріплених оболонок на пружній основі використовується варіаційний принцип стаціонарності Гамільтона –Остроградського, згідно якого

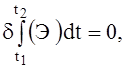(3)

Після стандартних перетворень в варіаційному функціоналі (3), з врахуванням співвідношень (2), отримаємо наступні системи диференціальних рівнянь:

– рівняння коливань гладких оболонок обертання з врахуванням пружної основи

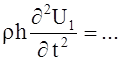, …. (4)

– рівняння коливань для -го ребра

, …. (5)

Рівняння коливань (4) –(5) доповнюються відповідними граничними та початковими умовами.

Також в другому розділі наведено постановку зв’язаної задачі оболонка – ґрунтове середовище.

Рівняння руху ґрунтового середовища приймаються у вигляді

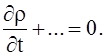, …. (6)

Рівняння стану ґрунтового середовища приймається в рамках нелінійної рідкої трьохкомпонентної моделі ґрунтів В.М. Ляхова

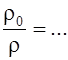, (7)

де зміст компонент по об’єму ; величини з індексом 1 відносяться до газоподібної компоненти, з індексом 2 відносяться до рідкої компоненти; з індексом 3 - до твердої компоненти; - показники ізентроп в газоподібній, рідкій і твердій компонентах середовищах; - швидкості звуку у відповідних компонентах середовища при атмосферному тиску; - густини компонентів середовища.

Рівняння коливань оболонки, яка взаємодіє із ґрунтовим середовищем має вигляд

, (8)

З метою оцінки впливу зовнішнього середовища на розповсюдження гармонійних хвиль у конструктивно-ортотропній моделі підкріпленої циліндричної оболонки на двохпараметричній основі Пастернака проведене аналітичне дослідження. Для лінійного варіанту рівнянь (4) для циліндричної оболонки вдалося виключити функцію 1 кута повороту нормалі до серединної поверхні і отримати систему рівнянь відносно переміщення uі прогину w. Відкинувши в цих рівняннях праві частини, отримаємо однорідне рівняння для дослідження розповсюдження гармонійних хвиль, які будемо шукати у вигляді:

; , (9)

де k– хвильове число, циклічна частота = Vk, V – швидкість гармонійних хвиль.

Підставивши (9) в отримане однорідне рівняння і скоротивши на sin(kx-t) і cos(kx-t), отримаємо однорідну систему рівнянь відносно U і W. Щоб ця система мала ненульовий розв’язок необхідно щоб її визначник дорівнював нулю. З цієї умови маємо дисперсійне рівняння:

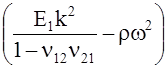…..…= 0. (10)

Проведемо асимптотичне дослідження можливих розв’язків цього рівняння: для випадку, коли довжина хвилі набагато більше ніж поперечний переріз оболонки то k0 -маємо стержень:

(11)

Оболонка без постелі має стержневу швидкість, а з абсолютно жорсткою постіллю - пластинчату.