Реферат: Основні поняття та визначення ЕЕГ Ряд та інтеграл Фурє

, (4)

. (5)

Величина виражає середнє значення функції за період, вона називається часто постійною складовою і обчислюється за формулою

. (6)

Чудовою властивістю ряду Фур'є є те, що якщо взяти кінцеве число членів ряду, тобто апроксимувати періодичну функцію тригонометричним поліномом, представивши її у вигляді

,

то для будь-якого можна отримати найменше квадратичне відхилення від точного значення , якщо коефіцієнти визначені за формулами (4), (5), (6). Із збільшенням числа членів наближення, зрозуміло, поліпшується, і в границях при наближена рівність переходить у точну.

Ряд Фур'є може бути також записаний у комплексній формі в такий спосіб:

, (7)

де

; ; .

Величина 2 є комплексна амплітуда, величина знаходиться за формулою

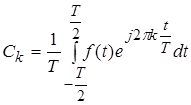, (8)

Підсумовування в (7) ведеться за всіма цілими , як позитивними, так і негативними, включаючи і нуль. Для того, щоб повернутися від (1) до (2) чи (3), потрібно згадати, що дійсна частина кожного доданка під знаком суми (7) парна стосовно , а уявна частина – непарна. Надалі переважно користуватимемось компактною формою (7).

Ряд Фур'є дає розкладання періодичної функції за тригонометричними функціями. Це розкладання може бути узагальнено і на випадок неперіодичної функції. Неточний, але наочний шлях до одержання розкладання Фур'є неперіодичної функції полягає в застосуванні граничного переходу при . Дійсно, неперіодичну функцію можна розглядати як граничний випадок періодичної функції при необмежено зростаючому періоді. Візьмемо формулу (7) і підставимо в неї значення з (8)

.

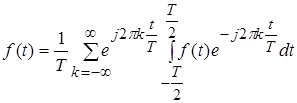Перейдемо до границі, спрямовуючи . Замість введемо кругову основну частоту

.

Ця частота є частотним інтервалом між сусідніми гармоніками, частоти яких дорівнюють . При граничному переході зробимо заміну за такою схемою

, , ,

де – поточна частота, що змінюється безупинно;

– її прирощення.

Сума перейде в інтеграл, і ми одержимо:

, (9)

чи

, (10)

де

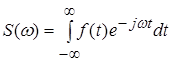. (11)

Формули (10) і (11) є основними формулами теорії спектрів. Вони являють собою пари перетворень Фур'є, що пов'язують між собою дві функції: дійсну функцію часу і комплексну функцію частоти . Формула (10) являє собою інтеграл Фур'є в комплексній формі. Зміст цієї формули полягає в тому, що функція представлена сумою синусоїдальних складових. Але функція передбачається неперіодичною, тому вона може бути представлена тільки сумою нескінченно великого числа нескінченно малих коливань, нескінченно близьких за частотою. Комплексна амплітуда кожного окремого коливання нескінченно мала, вона дорівнює