Реферат: Основні поняття та визначення ЕЕГ Ряд та інтеграл Фурє

Частотний інтервал між двома сусідніми коливаннями також нескінченно малий; він дорівнює .

Якщо ряд Фур'є являє собою періодичну функцію сумою хоча і нескінченного числа синусоїд, але з частотами, що мають визначені дискретні значення, то інтеграл Фур'є подає неперіодичну функцію сумою синусоїд з безперервною послідовністю частот. У складі неперіодичної функції є всі частоти.

Одна з особливостей, що відрізняє інтеграл Фур'є від ряду Фур'є, полягає в тому, що ряд Фур'є подає періодичну функцію як суму періодичних складових, тоді як інтеграл Фур'є – неперіодичну функцію сумою періодичних складових. Отже, у випадку інтеграла Фур'є сумі не притаманні властивості своїх доданків, і цю обставину необхідно враховувати у міркуваннях загального характеру про спектральне розкладання Фур'є.

Зазначимо насамкінець, що формулу (10) можна записати в дійсній формі; тоді інтегрування проводитиметься тільки по позитивних частотах. Увівши позначення

,

одержимо (з огляду на те, що А – парна, а В – непарна функція)

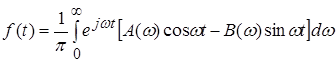. (13)

Можна одержати ще один запис формули (10), подавши її у вигляді

.

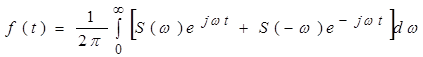У квадратних дужках поставлена сума сполучених величин, що дорівнює подвоєній дійсній частині. Тому

.
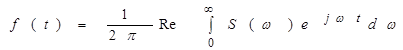