Реферат: Основные матмодели в теории надежности. Выбор числа показателей надежности. Достоверность статистической оценки показателей надежности

Министерство образования Республики Беларусь

Белорусский государственный университет информатики и

радиоэлектроники

кафедра РЭС

РЕФЕРАТ

на тему:

«Основные матмодели в теории надежности. Выбор числа показателей надежности. Достоверность статистической оценки показателей надежности»

МИНСК, 2008

Основные математические модели, используемы в теории надежности

В приведенных выше математических соотношениях зачастую использовалось понятие плотности вероятности и закон распределения.

Закон распределения - устанавливаемая определенным образом связь между возможными значениями случайной величины и соответствующими их вероятностями.

Плотность распределения (вероятностей) - широко распространенный способ описания закона распределения

Распределение Вейбулла

Распределение Вейбула является двухпараметрическим распределением. Согласно этому распределению плотность вероятности момента отказа

(1)

где δ - параметр формы (определяется подбором в результате обработки экспериментальных данных, δ > 0);

λ - параметр масштаба,

От значения коэффициента формы во многом зависит график функции плотности вероятности.

Интенсивность отказов определяется по выражению

(2)

Вероятность безотказной работы

(3)

Отметим, что при параметре δ = 1 распределение Вейбулла переходит в экспоненциальное, а при δ = 2 - в распределение Рэлея.

При δ <1 интенсивность отказов монотонно убывает (период приработки), а при δ >1 монотонно возрастает (период износа). Следовательно, путем подбора параметра δ можно получить, на каждом из трех участков, такую теоретическую кривую λ(t), которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности.

Экспоненциальное распределение

Как было отмечено экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы δ = 1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра λ = const . Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:

(4)

Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:

(5)

Таким образом, зная среднее время безотказной работы Т₁ (или постоянную интенсивность отказов λ), можно в случае экспоненциального распределения найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента t.

Распределение Рэлея

Плотность вероятности в законе Рэлея имеет следующий вид

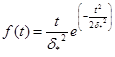(6)

где δ_* - параметр распределения Рэлея.

Интенсивность отказов равна:

. (7)

Характерным признаком распределения Рэлея является прямая линия графика λ(t), начинающаяся с начала координат.

Вероятность безотказной работы объекта в этом случае определится по выражению

(8)

Нормальное распределение (распределение Гаусса)

Нормальный закон распределения характеризуется плотностью вероятности вида

--> ЧИТАТЬ ПОЛНОСТЬЮ <--