Реферат: Основные механические характеристики материалов

Основы конструирования приборов

Реферат по теме

Основные механические характеристики материалов

Студента группы ИУ 3-32

Кондратова Николая

Диаграмма растяжения

Построение диаграммы растяжения-сжатия является основной задачей испытаний на растяжение-сжатие. Для этих испытаний используются цилиндрические образцы; полученные диаграммы являются зависимостью между силой, действующей на образец, и его удлинением. На рис. 1 показана типичная для углеродистой стали диаграмма испытания образца в координатах P , D l . Кривая условно может быть разделена на четыре зоны.

Зона ОА носит название зоны упругости. Здесь материал под­чиняется закону Гука и

???. 1.

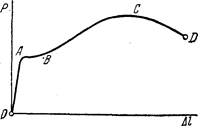Удли­нения D l на участке ОА очень малы, и прямая ОА, будучи вы­черченной в масштабе, совпадала бы в пределах ширины линии с осью ординат. Величина силы, для которой остается справедли­вым закон Гука, зависит от размеров образца и физических свойств материала.

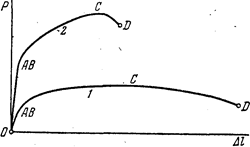
Зона АВ называется зоной общей текучести, а. участок АВ диаграммы — площадкой текучести. Здесь происходит существен­ное изменение длины образца без заметного увеличения нагрузки. В большинстве случаев при испытании на растяжение и сжатие площадка АВ не обнаруживается, и диаграмма растяжения образца имеет вид кривых, показанных на рис. 2. Кривая 1 ти­пична для алюминия и отожженной меди, кривая 2 — для высоко­качественных легированных сталей.

Зона ВС называется зоной упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более мед­ленным (в сотни раз), чем на упругом участке. В стадии упрочнения на образце намечается место будущего разрыва и начинает образо­вываться так называемая шейка — местное сужение образца (рис.3). По мере растяжения об­разца утонение шейки прогрессирует. Когда от­носительное уменьшение площади сечения срав­няется с относительным возрастанием напряже­ния, сила Р достигнет максимума (точка С). В дальнейшем удлинение образца происходит с уменьшением силы, хотя среднее напряжение в поперечном сечении шей­ки и возрастает. Удлинение образца носит в этом случае местный характер, и поэтому участок кривойCD называется зоной местной текучести. ТочкаD соответствует разрушению образца. У многих материалов разрушение происходит без заметного образования шейки.

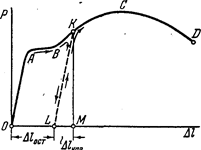
Если испытуемый образец, не доводя до разрушения, разгру­зить (точка К рис. 4), то в процессе, разгрузки зависимость между силой Р и удлинением Dl изобразится прямой К L (рис. 4). Опыт показывает, что эта прямая параллельна прямой ОА.

Рис. 2

При разгрузке удлинение полностью не исчезает. Оно уменьшается на величину упругойчасти удлинения (отрезокLM). ОтрезокOL представляет собой остаточное удлинение. Его называют также пластическим удлинением, а соответствующую ему деформацию — пластической деформацией. Таким образом,

ОМ=Dlупр + Dlост.

Соответственно

e =eупр + eост

Если образец был нагружен в пределах участка ОА и затем раз­гружен, то удлинение будет чисто упругим, и Dlост = 0.

Рис. 3

При повторном нагружении образца диаграмма растяжения при­нимает вид прямойLK и далее — кривойKCD (рис.4), как будто промежуточной разгрузки и не было.

Если взять два одинаковых образца, изготовленных из одного и того же материала, причем один из образцов до испытания нагружению не под­вергается, а другой — был пред­варительно нагружен силами, вызвавшими в образце остаточ­ные деформации.

Рис. 4

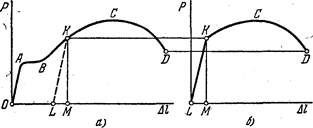
Испытывая первый образец, мы получим диаграмму растя­женияOABCD, показанную на рис. 5, а. При испытании вто­рого образца отсчет удлинения будет производиться от ненагруженного состояния, и остаточное удлинение OL уч­тено не будет. В результате по­лучим укороченную диаграмму LKCD (рис. 5, б). Отрезок МК соответствует силе предваритель­ного нагружения. Таким образом, вид диаграммы для одного и того же материала зависит от степени начального нагружения (вытяжки), а само нагружение выступает теперь уже в роли неко­торой предварительной технологической операции. Весьма сущест­венным является то, что отрезок LK (рис. 5,б) оказывается больше отрезка ОА. Следовательно, в результате предварительной вытяжки материал приобретает способность воспринимать без остаточных деформаций большие нагрузки.

Рис. 5

Явление повышения упругих свойств материала в результате предварительного пластического деформирования носит название наклепа, или нагартовки, и широко используется в технике.

Например, для придания упругих свойств листовой меди или ла­туни, ее в холодном состоянии прокатывают на валках. Цепи, тросы, ремни часто подвергают предварительной вытяжке силами, превыша­ющими рабочие, с тем, чтобы избежать остаточных удлинений в даль­нейшем. В некоторых случаях явление наклепа оказывается нежела­тельным, как, например, в процессе штамповки многих тонкостен­ных деталей. В этом случае для того, чтобы избежать разрыва листа, вытяжку производят в несколько ступеней. Перед очередной опера­цией вытяжки деталь подвергается отжигу, в результате которого наклеп снимается.

Основные механические характеристики материала

Для того, чтобы оценить свойства не образца, а материала, перестраивается диаграмма растяжения P = f (Dl) в коорди­натах s и e. Для этого уменьшим вF раз ординаты ивl раз абс­циссы, где F и l — соответственно площадь поперечного сечения и рабочая длина образца до нагружения. Так как эти величины по­стоянны, то диаграмма s =f (e) имеет тот же вид, что и диаграмма растяжения, но будет характеризовать уже не свойства образца, а свойства ма­териала.

Наибольшее напряже­ние, до которого матери­ал следует закону Гука, называется пределов про­порциональности (sn).

Величина предела пропорциональности за­висит от той степени точности, с которой начальный участок диаграммы можно рассмат­ривать как прямую. Степень отклонения кривой s = f (e) от прямой s = Е e определяют по величине угла, который составляет касатель­ная к диаграмме с осьюs. В пределах закона Гука тангенс этого угла определяется величиной 1/E . Обычно считают, что если вели­чина de/ds оказалась на 50% больше чем 1/Е, то предел пропор­циональности достигнут.

Упругие свойства материала сохраняются до напряжения, на­зываемого пределом упругости (s_у ) --- наибольшего напряжения, до которого материал не получает остаточных деформаций.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--