Реферат: Основные положения теории переходных процессов

– классический, основанный на составлении и решении дифференциальных уравнений;

– операторный, основанный на применении преобразования Лапласа;

– временной, использующий переходные и импульсные характеристики;

– частотный, базирующийся на спектральном представлении воздействия (преобразование Фурье).

Укажем, что последних три метода применимы только для линейных электрических цепей, поскольку в их основе лежит метод наложения (суперпозиции).

Сущность классического метода анализа переходных колебаний в электрических цепях

Переходные процессы в электрических цепях описываются уравнениями, составленными на основании законов Кирхгофа для мгновенных значений напряжений и токов. Эти уравнения для различных цепей после соответствующих преобразований могут быть приведены к какому-либо из следующих видов:

1) ;

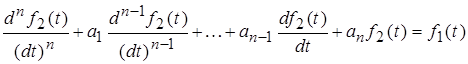2) ;

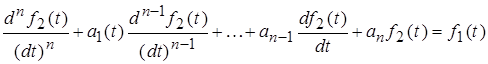3) .

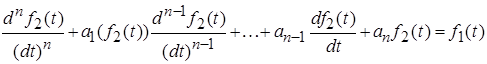Первое уравнение – линейное, с постоянными коэффициентами характеризует линейную цепь.

Второе, в котором, по крайней мере, один из коэффициентов (в данном случае ) является функцией времени, описывает линейную цепь с переменными параметрами (т. е. параметрические цепи).

Третье, в котором хотя бы один из коэффициентов (в данном случае ) является функцией , описывает нелинейную цепь и является, в отличие от первых двух, нелинейным дифференциальным уравнением.

Рассмотрим пример.

Пусть на последовательный контур (рис. 5), находящийся при нулевых начальных условиях в момент посредством замыкания ключа начинает действовать источник напряжения величиной . Требуется определить реакции.

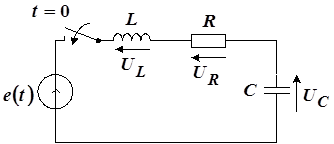
Рис. 5

Составим уравнение по второму закону Кирхгофа:

или

. (1)

Пусть все элементы цепи линейны. Тогда уравнение (1) преобразуется к виду:

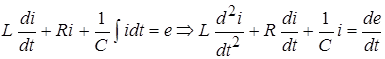
или

,

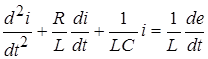где: ;

;

; .

Получено линейное, в общем случае неоднородное дифференциальное уравнение второго порядка, которое решается относительно известными из математики методами.

Аналогичное уравнение получается и для параметрической цепи. Пусть теперь цепь является нелинейной, например, допустим, что индуктивность является функцией тока, т.е. .