Реферат: Основные свойства и методы расчета линейных цепей постоянного тока

рис. 2.8.1

1) Эквивалентные преобразования пассивной части схемы

Заменим ветвь аб с последовательным соединением элементов одним эквивалентным сопротивлением , так чтобы и остались прежними.

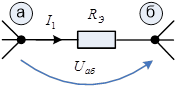
рис. 2.8.2

По второму закону Кирхгофа:

- согласно рис. 2.8.1 , тогда

- согласно рис. 2.8.2 , где

Заменим ветви между точками аб одним эквивалентным сопротивлением рис. 2.8.3

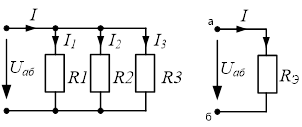
рис. 2.8.3

По первому закону Кирхгофа для исходной схемы (см. рис. 2.8.2)

;

По закону Ома: , ,

Для эквивалентной схемы запишем:

, где

2) Эквивалентные преобразования активной части схемы

Ранее мы выяснили, что любую часть схемы с двумя зажимами можно заменить эквивалентным генератором с параметрами , , .

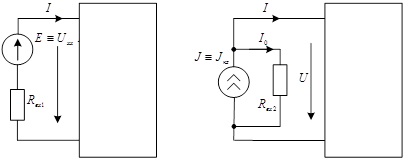
По второму закону Кирхгофа (рис. 2.8.4).

.

По первому закону Кирхгофа: , , тогда (см. рис. 2.8.5).

Сравнивая два выражения, приходим к выводу, что замена будет эквивалентной с точки зрения режима не преобразованной цепи, если выбрать , , следовательно .

3) Устранение из схемы ветви типа Е

Этот прием бывает полезен, когда схема содержит несколько ветвей типа E не соединенных между собой, а очень хочется писать уравнение метода узловых потенциалов.

Пусть есть схема с ветвью типа E, которую мы хотим устранить, но так, чтобы режим в остальных ветвях не изменился должны остаться неизменными токи в остальных ветвях. Для этого необходимо сохранить такую же систему уравнений.

Включим во все ветви, соединенные с одним из узлов устраняемой ветви, дополнительные источники ЭДС по величине равные устраняемой ЭДС и направленные все одинаково относительно рассматриваемого узла. Дополнительные источники ЭДС должны быть направлены так, чтобы в устраняемой ветви дополнительный источник ЭДС оказался включенным на встречу имевшейся.

Пример: