Реферат: Основные цели, определения и принципы математического моделирования, виды моделей

В соответствии с выбранной стратегией с учетом возможных ошибок при ее осуществлении производится выдача ЧО управляющих воздействий. Управляющие воздействия являются случайными событиями, которые характеризуются временем воздействия (моментами начала и конца воздействия) и величиной (уровнем) воздействия. Эти характеристики являются случайными величинами.

Случайным называется событие, которое при осуществлении определенных условий, может либо произойти, либо не произойти. Вероятность события есть численная мера степени объективной возможности этого события.

Случайная величина – величина, которая может принять какое-либо неизвестное заранее значение из некоторого интервала, зависящее от случайных причин, которые не могут быть учтены. Случайные величины могут быть дискретными и непрерывными. [8]

Главной вероятностной характеристикой случайной величины является закон распределения.

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения может быть представлен в виде ряда распределения, функции распределения и плотности распределения.

Таблица, в которой перечислены все возможные значения случайной величины и соответствующие им вероятности называется рядом распределения.

X	x1	x2	x3	...	xN
p(X)	p1	p2	p3	...	pN

Вероятность того, что случайная величина примет значение меньшее некоторого x , является функцией, зависящей от x , и называется функцией распределения или интегральным законом распределения.

Функция распределения является универсальным законом распределения, т.к. существует и для дискретных, и для непрерывных случайных величин.

Производная от функции распределения характеризует плотность распределения вероятности по случайной величине и называется плотностью распределения вероятности или дифференциальным законом.

Основными числовыми характеристиками случайной величины являются математическое ожидание (МО), дисперсия и среднеквадратическое отклонение (СКО).

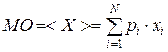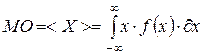МО характеризует положение случайной величины на числовой оси и определяется как и для дискретных и непрерывных величин соответственно.

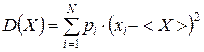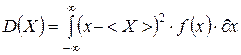Дисперсия характеризует рассеяние случайной величины около МО, является квадратом отклонения случайной величины от ее МО и определяется как и для дискретных и непрерывных величин соответственно.

СКО определяется как квадратный корень из дисперсии и служит для большей наглядности рассеяния величины.

Ошибки управления зависят от множества случайных факторов. При равном влиянии множества случайных факторов на величину можно говорить о нормальном законе ее распределения [11]. Плотность распределения последнего описывается формулой

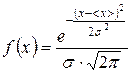, (6)

где - МО и СКО случайной величины, соответственно.

Внешний вид нормальной плотности распределения представлен на рис. 5.

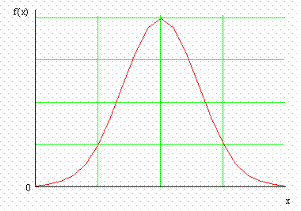
Рис. 5 Нормальный закон распределения.

Управляющие воздействия представляют собой вектора, обладающие следующим набором характеристик

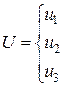
где u₁ – время начала воздействия, u₂ – время конца воздействия, u₃ – величина (уровень) воздействия. Эти характеристики - случайные величины, распределение которых также подчинено нормальному закону. МО величин являются их значения в точности соответствующие выбранной стратегии. СКО связаны с отклонениями от выбранной стратегии функциональной зависимостью. Отклонения от выбранной стратегии представляют собой суммарные ошибки оператора, вызванные задержкой реакции, рассогласованием, ошибочной информацией о положении рабочих органов ПТМ и груза. Они нормируются в зависимости от квалификации оператора.

разряд	I	II	III	...
величина ошибки				...

При моделировании характеристики управляющих воздействий определяются либо с учетом распределения их вероятности, либо по зависимости

, (7)

Для получения достоверных и точных результатов необходимо использовать стохастическую модель. Данные, полученные с помощью машинных экспериментов, обрабатываются методами математической статистики [10].

Пусть есть величина X равномерно распределенная на интервале [0,1]. Для преобразования равномерно распределенных случайных чисел в числа, распределенные по нормальному закону, воспользуемся преобразованием

, (8)

где - МО величины, - СКО величины.

2.4 Объект моделирования – окружающая среда

Окружающая среда воздействует на ЧО и ПТМ. Эти воздействия учитываются множеством Y , в котором Y₁ – воздействия на ЧО, влияющие, в основном, на его способность воспринимать информацию и выдавать управляющие воздействия, Y₂ – воздействия на ПТМ, складывающиеся из воздействий, меняющих свойства материалов, из которых изготовлены элементы ПТМ, воздействий, меняющих характеристики элементов ПТМ и нагрузок. В зависимости от микроклимата района, сейсмической активности и т.д. выделяют несколько зон [32, 33]. Каждой зоне соответствуют свои параметры воздействий на ПТМ, которые случайны. Основной интерес представляют силовые воздействия окружающей среды на ПТМ.

1) Ветровые нагрузки являются распределенными по наветренной площади нагрузками, действующими горизонтально и включающими статическую и динамическую составляющие.

Наветренной площадью называется проекция площади на плоскость, перпендикулярную направлению ветрового потока (Рис. 6).

Рис. 6 Наветренная площадь

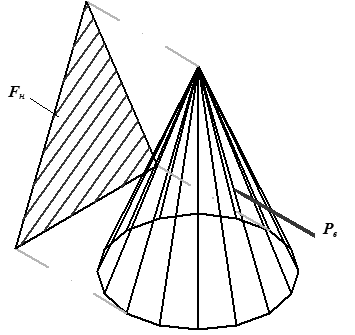
Ветровую нагрузку можно рассматривать как сосредоточенную силу, приложенную в центре тяжести наветренной площади. Положение центра тяжести сечения (площади) определяется по известным зависимостям

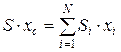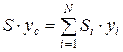, , (9)

и при переходе к предельным значениям

() , , (10)