Реферат: Основы экономного кодирования

6

6

12

110

З

7

7

13

111

Таблица 1

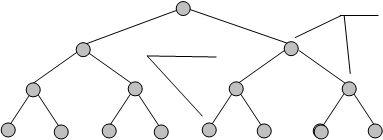
Другим наглядным и удобным способом описания кодов является их представление в виде кодового дерева (рис..1).

Корень Узлы 0 1 Вершина 0 1 0 1 0 1 0 1 0 1 0 1 А Б В Г Д Е Ж З 1 2 3 4 5 6 7 8 Рис. 4.

Рис. 1

Для того, чтобы построить кодовое дерево для данного кода, начиная с некоторой точки - корня кодового дерева - проводятся ветви - 0 или 1. На вершинах кодового дерева находятся буквы алфавита источника, причем каждой букве соответствуют своя вершина и свой путь от корня к вершине . К примеру, букве А соответствует код 000, букве В – 010, букве Е – 101 и т.д.

Код, полученный с использованием кодового дерева, изображенного на рис. 1, является равномерным трехразрядным кодом .

Равномерные коды очень широко используются в силу своей простоты и удобства процедур кодирования-декодирования: каждой букве – одинаковое число бит; принял заданное число бит – ищи в кодовой таблице соответствующую букву.

Наряду с равномерными кодами могут применяться и неравномерные коды, когда каждая буква из алфавита источника кодируется различным числом символов, к примеру, А - 10, Б – 110, В – 1110 и т.д.

Кодовое дерево для неравномерного кодирования может выглядеть, например, так, как показано на рис. 2.

Рис. 2

При использовании этого кода буква А будет кодироваться, как 1, Б - как 0, В – как 11 и т.д. Однако можно заметить, что, закодировав, к примеру, текст АББА = 1001 , мы не сможем его однозначно декодировать, поскольку такой же код дают фразы: ЖА = 1001, АЕА = 1001 и ГД = 1001. Такие коды, не обеспечивающие однозначного декодирования, называются приводимыми, или непрефиксными, кодами и не могут на практике применяться без специальных разделяющих символов. Примером применения такого типа кодов может служить азбука Морзе, в которой кроме точек и тире есть специальные символы разделения букв и слов. Но это уже не двоичный код.

Однако можно построить неравномерные неприводимые коды, допускающие однозначное декодирование. Для этого необходимо, чтобы всем буквам алфавита соответствовали лишь вершины кодового дерева, например, такого, как показано на рис. 3. Здесь ни одна кодовая комбинация не является началом другой, более длинной, поэтому неоднозначности декодирования не будет. Такие неравномерные коды называются префиксными.
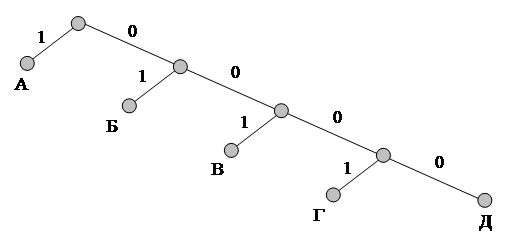