Реферат: Основы химической термодинамики
![]() (1.4) или давления
(1.4) или давления ![]() , (1.5)
, (1.5)
где Bi , Bi ' - i -ые вириальные коэффициенты, которые зависят от температуры.
Уравнение состояния идеального газа и вириальное уравнение состояния реального газа можно вывести методами статистической термодинамики.
Иногда уравнения состояния реальных газов записывают через так называемые приведенные переменные , которые определяют через параметры критического состояния газов: pr = p /p кр , Vr = V / V кр , Tr = T / T кр , где критические параметры определяются как координаты точки перегиба на изотерме реального газа:
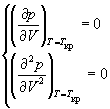
ПРИМЕРЫ
Пример 1-1. Докажите, что при больших объемах уравнение Ван-дер-Ваальса переходит в уравнение идеального газа.
Решение . Уравнение Ван-дер-Ваальса:
![]() .
.
При больших объемах вторым слагаемым в правой части можно пренебречь: a /V 2 ![]() 0. В знаменателе первого слагаемого можно пренебречь постоянной b : V -b
0. В знаменателе первого слагаемого можно пренебречь постоянной b : V -b ![]() V . В пределе получаем уравнение идеального газа:
V . В пределе получаем уравнение идеального газа:
![]() .
.
Пример 1-2. Найдите вириальные коэффициенты Bi для газа, подчиняющегося уравнению Ван-дер-Ваальса.
Решение . В уравнении Ван-дер-Ваальса выделим сомножитель RT /V :
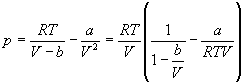
Если разложить первое слагаемое в скобке в ряд по степеням b /V , получим:
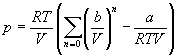
Из этого разложения следует, что второй вириальный коэффициент газа Ван-дер-Ваальса зависит от температуры:
![]() , а остальные - постоянны:
, а остальные - постоянны: ![]() .
.
Пример 1-3. Найдите критические параметры и приведенное уравнение состояния для газа Дитеричи (I уравнение).
Решение . Запишем уравнение Дитеричи в виде:
![]()
и продифференцируем левую и правую часть этого уравнения два раза по объему при постоянной температуре:
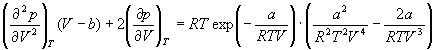
и учтем, что в критической точке первая и вторая производная равны 0:
![]() ,
,
откуда находим: ![]() .
.
Если продифференцировать обе части уравнения состояния по объему один раз с учетом равенства нулю первой производной, то можно найти второе соотношение между критическими объемом и температурой:
![]() ,
,
откуда
![]() .
.
Подставляя сюда первое найденное соотношение для критических параметров, получим:
![]()
![]()
И, наконец, подставляя эти параметры в уравнение состояния, находим критическое давление:
![]() .
.
Для вывода приведенного уравнения состояния подставим в уравнение Дитеричи приведенные переменные: