Реферат: Основы химической термодинамики
В результате получаем приведенное уравнение Дитеричи, не содержащее индивидуальных параметров:
.
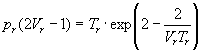ЗАДАЧИ
1-1. Приведите пример термодинамического процесса, который может совершаться как обратимо, так и необратимо. Назовите для этого процесса по одной функции состояния и перехода.
1-2. Приведите примеры систем со временем релаксации порядка: а) секунд; б) часов; в) десятилетий.
1-3. Изменение теплоты в зависимости от температуры и объема в некоторой системе описывается уравнением:
(C и R - постоянные). Является ли теплота функцией состояния в данном случае? Ответ обоснуйте.
1-4. Докажите, что при больших объемах первое уравнение Дитеричи переходит в уравнение идеального газа.
1-5. Найдите частные производные 
и 
для: а) идеального газа; б) газа Ван-дер-Ваальса; в) газа, подчиняющегося I уравнению Дитеричи. Докажите, что 
.
1-6. Используя вириальные разложения (1.4) и (1.5), найдите связь между вириальными коэффициентами B 2 , B 3 и B 2 ', B 3 '.
1-7. Найдите критические параметры и приведенные уравнения состояния для газов: а) Ван-дер-Ваальса; б) Бертло.
1-8. Предложено следующее уравнение состояния (для одного моля):
Выразите критические параметры через постоянные B и C и найдите фактор сжимаемости PV /RT в критической точке.