Реферат: Основы построения систем. Способы передачи и анализ телемеханических сигналов

Соотношения (2.1) и (2.2) являются парой преобразований Фурье, причем первое из них выражает так называемую спектральную плотность сигнала (частотный спектр).

Любой сигнал конечной длительности или периодический сигнал могут быть представлены совокупностью периодических (гармонических) составляющих (рис. 13) в соответствии с разложением в ряд Фурье.

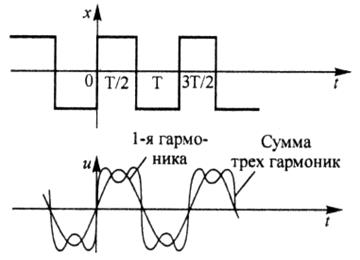Рис. 13. Представление сигналов гармоническими составляющими

Коэффициенты разложения определяются функционалами:

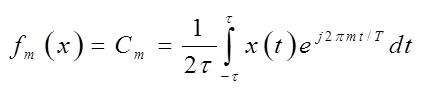
где:

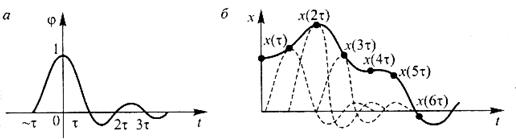
Другим широко используемым способом представления любого сигнала является его представление временным рядом, т.е. конечным набором функций, описывающих интерполирующий импульс (рис. 14, а) при разных его смещениях по оси времени (рис. 14, б). Обычно такой импульс удовлетворяет условиям:

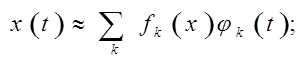
???. 14. ????????????? ???????? ????????? ?????

Сигналы с ограниченной частотой изменения представляют дискретным набором отсчетов через равностоящие промежутки времени (рис. 15) в соответствии с теоремой Котельникова (теорема отсчетов), т.е. для любого

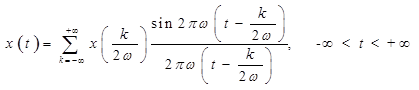
Кроме указанных способов представления произвольных сигналов существует множество других, например разложения по полиномам Лежандра, Чебышева, Лагерра, функциямБесселя, Хаара и др.

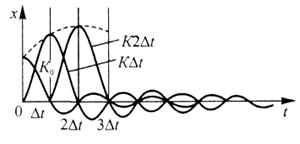
Рис. 15 Представление сигналов дискретными отсчетами

Таким образом, для описания любых детерминированных во времени сигналов существуют различные методы. Однако в реальных системах часто приходится иметь дело со случайными сигналами, т.е. с такими функциями времени, значения которых лежат в определенном диапазоне и появление любой из них имеет определенную вероятность (стохастический процесс) где рассматривается как вектор в гильбертовом пространстве, образуемом точками по параметру t.

В таких системах стремятся определить не конкретное значение сигнала (отдельная реализация), а вычислить статистические средние значения по отношению к случайным переменным (математическое ожидание). Тогда случайный процесс во времени характеризуется детерминированной во времени функцией от различных ожиданий, а не формой конкретных сигналов. В этом состоит принципиальное различие в описаниях детерминированных и случайных сигналов.

Для сравнительной оценки сигналов одного множества по каким-либо свойствам каждой паре элементов множества ставится в соответствие действительное положительное число, называемое расстоянием между элементами .

Расстояния во множестве, представляющем пространство сигналов, определяют по условному правилу, называемому метрикой данного пространства . Метрика должна удовлетворять следующим условиям:

т.е. расстояние неотрицательно;

т.е. расстояние от х до у равно расстоянию от у до х (симметрия);

т.е. длина одной стороны треугольника векторов не может быть больше суммы двух других.

Для одного и того же множества элементов по разным метрикам могут быть образованы разные метрические пространства. Например, если принять и то расстояние в трехмерном пространстве (Евклидова метрика)

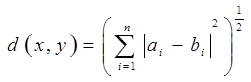
Из этого же множества элементов может быть образовано пространство, определяемое по метрике Хэмминга, т.е.

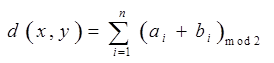
В этом случае расстояние между любой парой слов определяется числом несовпадающих символов (суммирование по модулю 2) по всем разрядам. Эта метрика широко применяется для сравнения кодов по возможностям обнаружения и исправления ошибок.

Кодирование . Сообщения, подлежащие передаче по каналу связи, должны быть представлены в форме, наиболее удобной для передачи по данному каналу. Таким образом, подразумевается преобразование одного исходного пространства сигналов в эквивалентное ему. Подобное преобразование проходит в два этапа. Первоначально из избыточного множества сигналовследует выделить подмножество , содержащее М нужных сигналов. Затем их необходимо поставить в однозначное соответствие с исходными сигналами. Первый этап может быть осуществлен различными способами, а второй — М! Таким образом, общее число возможных правил кодирования .