Реферат: Основы проектирования и конструирования машин
Ускорение точки C определяется из векторных уравнений:
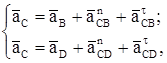(3)
где 
- векторы абсолютных ускорений точек, при чем 
; 
- векторы нормальных ускорений; 
- векторы тангенсальных ускорений.
Определим значения и длины отрезков нормальных ускорений:
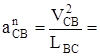(м/с2 ),
в масштабе плана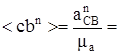 
(мм).
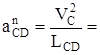(м/с2 ),
в масштабе плана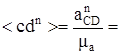 
(мм).
Выполним построения для нахождения точки C (рис.13, 15, 18):
1) Для этого из точки b плана ускорений откладываем параллельно звену BC отрезок 
(нормальное направление ускорения) по направлению в сторону движения от точки С к точке В. Перпендикулярно BC проводим через конец этого отрезка линию - тангенсальное направление ускорения.
2) Из полюса p плана ускорений откладываем параллельно звену CD отрезок 
(нормальное направление ускорения) по направлению в сторону движения от точки С к точке D. Перпендикулярно CD проводим через конец этого отрезка линию - тангенсальное направление ускорения.
3) Пересечением 2-линий тангенсальных направлений получится точка C – вектор 
.
4) Находим величину ускорения точки С из плана ускорений:
(м/c)
Построим ускорение точки Е для заданий №1,3 (рис.13, 18) :
Ход построения ускорения точки Е аналогичен скорости. Т.к. точка Е принадлежит звену CD, значит, направления ускорений точек С и Е совпадают, а длина вектора 
находится из пропорции:
; 
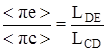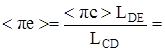(мм)
Откладываем из полюса 
параллельно вектору длину вектора 
- получаем точку E на плане ускорений.
Построим ускорение точки Е для задания №2 (рис.15) :
Ход построения ускорения точки Е аналогичен скорости, поэтому:
; 
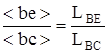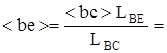(мм)
Находим величину ускорения точки E из плана:
(м/c)
Определим значение и длину отрезка на плане нормального ускорения 
:
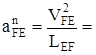(м/с2 ),
в масштабе плана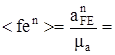 
(мм).
Выполним построения для нахождения ускорения точки F (рис.13, 15, 18):
1) Для этого из точки e плана ускорений откладываем параллельно звену EF отрезок 
(нормальное направление ускорения) по направлению в сторону движения от точки F к точке E. Перпендикулярно EF проводим через конец этого отрезка линию - тангенсальное направление ускорения.
2) Через полюс p плана ускорений проводим линию параллельную оси x-x.
3) Пересечением 2-х направлений получится точка F – вектор 
.