Реферат: Отображение АСД на СДХ

(Вершины)

ì 1, если X инцендентно U и Xявляется концом дуги U

s = í -1, если X инцендентно U и Xявляется началом дуги U

î 0, в противном случае.

Степень вершины - число дуг входящих (в) и выходящих (из) данной вершины (инцендентных данной вершине).

Степень захода (исхода) - число дуг входящих (выходящих) в (из) данную вершину.

Граф называется регулярным, если степень его вершин постоянна.

Последовательность вершин графа X...Xназывается цепью, если для

" (X, X) Î U, т.е. существуют дуги по которым можно перейти от X к X, от X к X и т.д.

Последовательность вершин графа называется путем, если для

" (X, X) Î U или (X, X) Î U.

Всякая цепь - путь, но не всякий путь - цепь.

Если в цепи X=X, то такая цепь называется цикл.

Граф называется слабосвязанным, если для " его двух вершин существует путь их соединяющий, без относительно их ориентации.

Граф называется сильносвязанным, если для " его двух вершин существует путь их соединяющий, с учетом их ориентации.

Вес пути X ... X - сумма весов дуг этого пути.

m (X ... X) =m (x, x)

Операции:

- вставить вершину,

- удалить вершину,

- вставить дугу,

- удалить дугу и т.д.

С точки зрения графа строка это цепь.

Дерево

Дерево - связный ациклический граф.

Одна вершина в дереве обязательно имеет степень захода 0. Эта вершина - корень дерева. Листья дерева - вершины, имеющие степень исхода равную 0.

Для любой вершины дерева (кроме корня) степень захода равна 1.

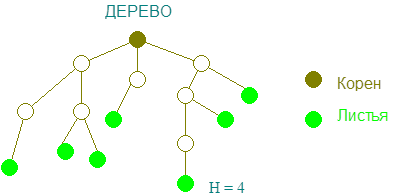
Деревья могут быть ориентированные и неориентированные.

Высота дерева (H) - самый длинный путь из корня к листу.